Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга. ![\frac{3 \sqrt[]{3}r^{2}}{\pi r^{2}}=\frac{3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/07e0a.png)
Пусть площадь круга х, тогда площадь треугольника (по условию) ![x+27\sqrt[]{3}-9\pi](/tpl/images/0144/4450/08b8d.png)
с одной стороны и ![\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/56410.png)
с другой.
Получим уравнение ![x+27\sqrt[]{3}-9\pi=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/99a9d.png)
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
![\frac{x\pi}{\pi}+\frac{\pi27\sqrt[]{3}}{\pi}-\frac{9\pi^{2}}{\pi}=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/4f04e.png)
![x\pi}+\pi27\sqrt[]{3}-9\pi^{2}=x3 \sqrt[]{3}](/tpl/images/0144/4450/57c86.png)
Вынесем 3 корня из трех - Пи за скобки и получим
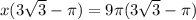
площадь круга = 9Пи
Найдем радиус круга
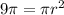
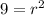
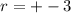
Т к радиус не может быть отрицательным то он равен 3
Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга.
Пусть площадь круга х, тогда площадь треугольника (по условию) с одной стороны и с другой.
Получим уравнение
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
Вынесем 3 корня из трех - Пи за скобки и получим
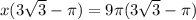
площадь круга = 9Пи
Найдем радиус круга
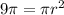
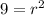
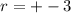
Т к радиус не может быть отрицательным то он равен 3
В уравнениях такого вида коэффициент к показывает крутизну (точнее тангенс угла) наклона графика функции к оси х (абсцисс), а величина в дает точку пересечения этим графиком оси у (ординат).
3х-4у+24=0
4у = 3х +24
у = (3/4)х + 6.
Уравнение х^2+у^2=25 - зто уравнение окружности в центре координат с радиусом, равным √25 = 5.
Для нахождения взаимного расположение прямой и окружности надо решить систему уравнений: 3х-4у+24=0 и х^2+у^2=25.
Совместное решение дает результат:
х₁ = -4; у₁ = 3;
х₂ = -44/25; у₂ = -117/25, то есть прямая пересекает окружность в двух точках.
2) Аналогично решается второе задание - в этом случае графики заданных уравнений не песекаются.