площадь равнобедренного треугольника равняется произведению высоты на половину длины основания. основание у нас есть 20см , надо узнать высоту. рисовать не буду, поэтому так напишу, треугольник АВС, основание будет АВ, вершина С. тогда высота СД. Высота образует прямоугольный треугольник ВСД, вот с ним и будем работать.
что мы про него знаем? - сторона ВС=136, сторона ВД=20/2=10. нам нужно узнать СД. треугольник прямоугольный, применяем теорему Пифагора( квадрат гипотенузы равен сумме квадратов катетов), получится ВС"=ВД"+СД", СД"=ВС"-ВД".
СД"=136"-10", Сд"= 18 496-100=18 396, СД=корень из 18396.
S= корень из 18396*10.
честно говоря, ответ мне не нравится. ты точно условие правильно переписал? какие то невкусные числа получаются
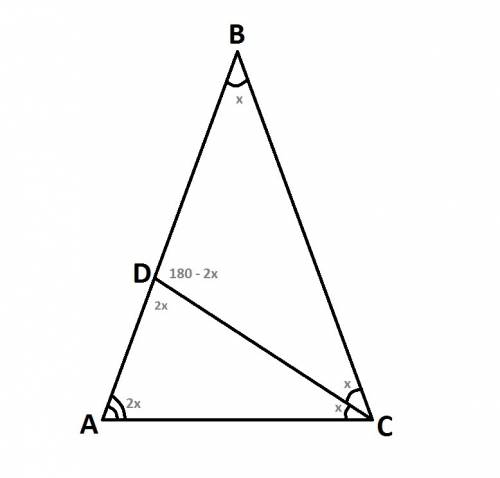
Пусть угол ACD равен x. По условию сказано, что угол ABC равен углу ACD, значит угол ABC равен x. Так как CD биссектриса, значит угол DCB равен углу ACD и равен x. По теореме об углах треугольника, угол BDC в треугольнике CDB равен 180 - x - x = 180 - 2x. По теореме о смежных углах, угол ADC равен 180 - (180 - 2x) = 180 - 180 + 2x = 2x. Так как треугольник ABC равнобедренный, угол BAC равен углу ACB (угол ACB = угол ACD + угол DCB = 2x). Получается, что угол BAC равен 2x. Так как угол BAC равен 2x, и угол ADC равен 2x, понятно что треугольник ADC равнобедренный (углы при основе равны). Следовательно AC = CD = 10 см. ответ: биссектриса CD равна 10 см.