а=18,
Р=2а+2b
54=36+2b
2b=18
b=9
S=18*9=162
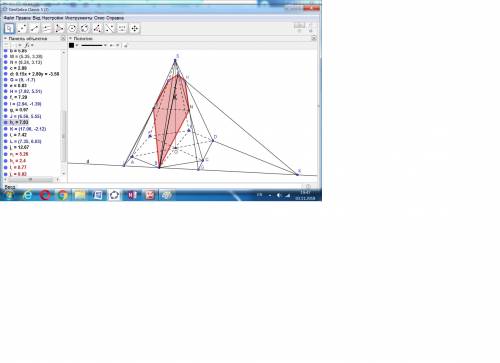
а) Сечение строится с использованием следа d, параллельного MN.
Затем до этой линии продлеваем стороны основания и через полученные точки и точки M и N проводим линии SD и SF.
Аналогично находим точку на ребре SE.
б) Деление высоты в точке К построенной плоскостью определяем по теореме Менелая. (SK/KO)*(2/1)*(1/1) = 1.
Отсюда (SK/KO) = (1/2).
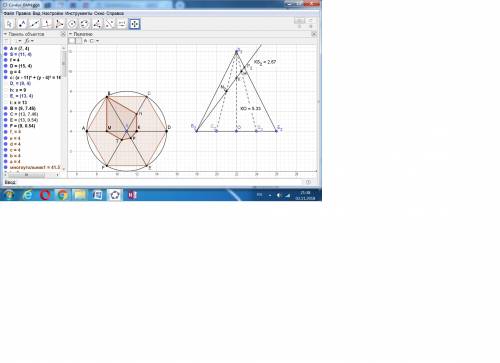
Для этого используем сечение пирамиды плоскостью BSE, на которое проецируется ребро SC.
В этой проекции ВС = СО по свойству шестиугольника, CN = NS по заданию.
Получаем треугольник CSO и секущая ВК.
Периметр равен P=2(a+b)
одна из сторон равна b=P/2-a
Площадь равна S=ab
S=a(P/2-a)
S=18*(54/2-18)=162 кв.м
ответ: 162 кв.м