Укажите номера верных утверждений: 1) образованные при пересечении двух параллельных прямых третьей накрест лежащие углы равны. 2) если биссектриса треугольника является его высотой, то этот треугольник равнобедренный. 3) треугольника со сторонами 2, 8, 11 не существует. 4) уравнением окружности с центром q(-2; -3) и радиусом 5 является уравнение (x-2)^2+(y-3)^2=25
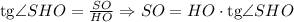
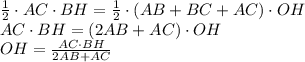
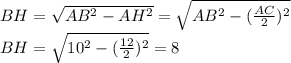
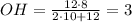
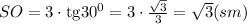
 см
см
2 правильное
3 правильное, так как сумма двух любых сторон не больше третьей стороны
4 неправильное. (х+2)^2+(х+3)^2=25