В задачах на построение используются только такие инструменты: циркуль и линейка.
По условию задачи у нас есть отрезок и угол. А так как у равнобедренного треугольника углы при основании равны, то нам нужно построить треугольник по стороне и двум прилежащим к ней углам - это одна из основных задач на построение (см. учебник по геометрии за 7 класс).
Построение.
1. Проводим прямую.
2. На прямой берем точку А и откладываем отрезок, равный данному (с циркуля, еще одна основная задача на построение). Получаем точку С.
3. От точки А откладываем угол, равный данному (с циркуля, еще одна основная задача на построение).
См. приложение
4. От точки С откладываем угол, равный данному (аналогично п. 3).
5. Стороны углов пересекутся в вершине В треугольника .
Искомый равнобедренный треугольник построен.
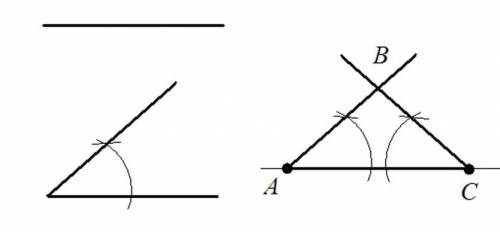
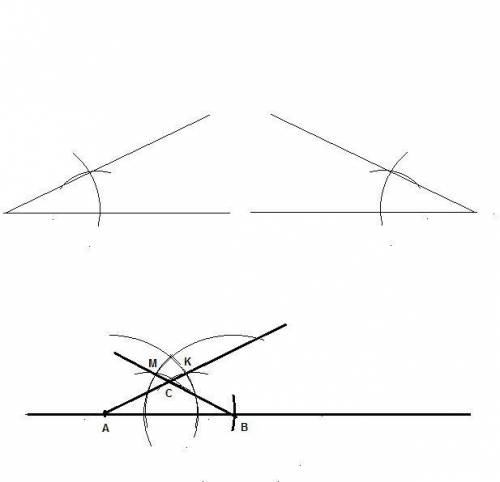
1. Рисуем прямую линию а и ставим на ней точку А.
2. Берем циркуль, раздвигаем ножки на длину основания, втыкаем его в точку А и рисуем дугу на прямой. Получаем точку В.
3. Втыкаем циркуль в вершину заданного угла и рисуем дугу, которая должна пересечь обе стороны заданного угла.
4. Вставляем циркуль в точку А и рисуем дугу такого же радиуса.
5. Втыкаем циркуль в одно пересечение на заданном углу и раздвигаем ножки на расстояние между пересечениями.
6. Втыкаем циркуль в точку пересечения на прямой и тем же радиусом ставим засечку на дуге, нарисованной из точки А.
Получили точку К пересечения двух дуг. Рисуем луч АК. Получился угол такого же размера, как и заданный.
7. Повторяем пункты 4 - 6 на точке В. Рисуем луч ВМ.
8. Лучи АК и ВМ где-то пересекутся. Это и есть точка С - третья вершина треугольника АВС.
Вот я на картинке постарался нарисовать, но в Paint нет клеток и точно нарисовать невозможно. Заданный угол я нарисовал два раза в зеркальном отражении, чтобы проще нарисовать дуги из А и из В.
Площадь треугольника равна половине произведения его сторон на синус угла между этими сторонами.
В нашем случае S = (1/2)AB*BC*Sinα или 3√3 = 2√3*3*Sinα.
Следовательно, Sinα = (3√3)/6√3 = 1/2.
Итак, угол В в треугольнике АВС равен 30°. Cos30° = √3/2.
По теореме косинусов находим сторону АС треугольника:
АС = √(АВ²+ВС²-2*АВ*ВС*Cos30) или
√(48+9-2*12√3*√3/2)=√21.
Ну, а радиус описанной около треугольника окружности находится по формуле: R = a*b*c/4S или в нашем случае R=4√3*3*√21/12√3 = √21.
ответ: радиус описанной около треугольника окружности равен √21.