Из прямоугольного треугольника ABD
AD^2=AB^2+BD^2=9+16=25
AD=5
Площадь основания равна 2*площадь ABD=2*(3*4/2)=3*4=12
AD параллельно BC, следовательно параллельно B1C1, поэтому AD принадлежит плоскости AB1C1, и это прямая пересечения плоскости основания с плоскостью AB1C1
Пусть BE высота в треугольнике ABD
Тогда угол B1EB это угол между плоскостью основания и плоскостью AB1C1, так как BE перпендикулярно AD, B1E перпендикулярно AD по теореме о трёх перпендикулярах.
Треугольник B1EB -- прямоугольный треугольник с углом 45 градусов, а следовательно, равнобедренный прямоугольный треугольник, поэтому B1B=BE
Чтобы найти высоту BE выразим площадь треугольника ABD двумя
площадь ABD = AB*BD/2 = AD*BE/2, отсюда
BE=AB*BD/AD=3*4/5=12/5=2,4
Площадь полной поверхности равна
2*площадь основания+площадь боковой поверхности
площадь боковой поверхности = периметр основания умножить на высоту
периметр основания = AB+BC+CD+AD=3+5+3+5=16
тогда площадь боковой поверхности 16*2,4=38,4
площадь полной поверхности
2*12+38,4=24+38,4=62,4
Сторона правильного шестиугольника равна радиусу описанной окружности, т.е. а = R.
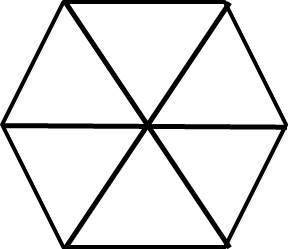
Т.к. проведя все радиусы в шестиугольнике, вписанном в окружность, мы разобьем его на 6 равносторонних треугольников (см. рис.), а площадь получившегося треугольника можно найти по формуле
1/2 · R · R · sin60° = 1/2 · R² · √3/2 = R²√3/4
(полный круг составляет 360°, тогда угол при вершине равностороннего треугольника будет равен 60°, а sin60° = √3/2), то площадь шестиугольника будет равна:
6 · R²√3/4 = 3R²√3/2 = 3 · 2²√3/2 = 6√3 (см²)
ответ: 6√3 см².
этапы построения слева направо
смотрим во вложении