АВСD- трапеция, АВ и DC - основания, AD=BC=6см - боковая сторона,
М лежит на стороне AD, N лежит на стороне BC, MN=10см - средняя линия .
P=AB+BC+CD+AD
MN=1/2(AB+CD)
6=1/2(AB+CD)
AB+CD=12 (2 боковые стороны)
P=12+10+10=32
1)Найдите координаты точки пересечения прямых, заданными уравнениями
x+2y-5=0
3x-y-8=0
x+2y-5=0
3x-y-8=0
х=5-2у
3(5-2у)-у-8=0
15-6у-у-8=0
-7у=-7
у=1
х=5-2*1=3
ответ:(3;1)
2) В каких точках пересекается с осями координат прямая заданная уравнением:
2x-5y+20=0
при х=0 2*0-5у+20=0 Итак, первая точка (0;4)
5у=20
у=4
при у=0 2х-5*0+20=0 Итак, вторая точка (10;0)
2х=20
х=10
ответ: (0;4), (10;0)
3)Прямые y=x+4, y=-2x+1 пересекаются в некоторой точке О, найдите ее координаты.
х+4=-2х+1
х+2х=1-4
3х=-3
х=-1
у(-1)=-1+4=3
ответ: (-1;3)
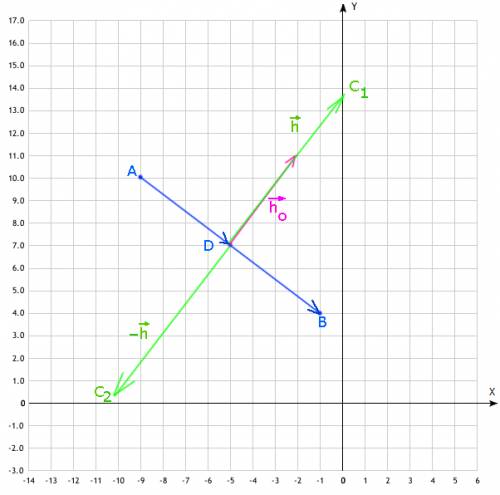
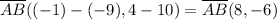 ;
; от точки A
от точки A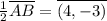 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: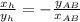 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 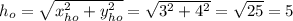 ;
;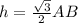 , т.к
, т.к 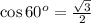 ;
;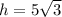 , а стало быть
, а стало быть  ;
;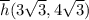 .
.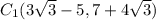 /// примечание:
/// примечание: 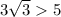 ;
;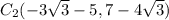 /// примечание:
/// примечание: 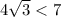 .
.
Чтобы найти среднюю линию трапецыи нужно найти суму двух её основ и поделить на два, отсюда сума её основ 10*2=20см. Так, как трапецыя равнобедренная, то сума её боковых сторон будет 6+6=12см. Отсюда периметр трапецыи 20+12=32см.
ответ:32см.