ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
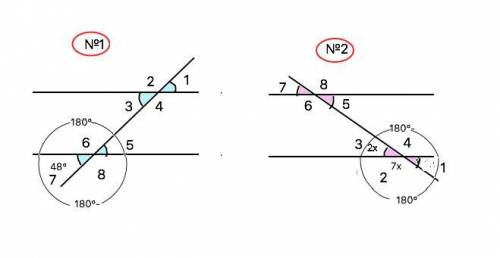
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
АВСД - прямоугольник. О - пересечение диагоналей ОК срединный перпендикуляр к диагонали ВД. Тогда по условию: КС = СД.
То есть тр. ДКС - прям, равноб. Значит его острые углы - по 45 гр.
СДК = 45 гр = ДКС
Угол ДКС - внешний для равнобедр. тр-ка ВКД (КД = ВК - по св-ву срединного перпенд)Значит: 2*КДВ = 45 гр.
Или угол КДВ = 22,5 гр.
Тогда угол СДО в тр. СОД равен:
СДО = 45 + 22,5 = 67,5 гр и равен ОСД (т.к тр.СОД - равнобедр)
В итоге находим искомый угол СОД = 180 - (67,5 + 67,5) = 45 гр.
ответ: 45 гр(острый) или 135 гр (тупой)