ответ: 6 целых 4/7
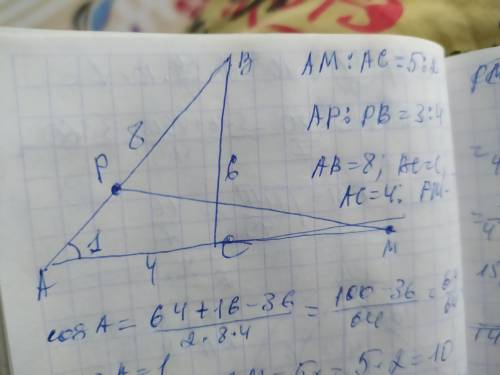
Объяснение: рассмотрим ∆АВС. В нём известны 3 стороны, и мы можем найти используя теорему косинусов угол А:
cosA=(AB²+AC²-BC²)/2×AB×AC=
=(8²+4²-6²)/2×8×4=(64+16-36)/64=64/64=1
cosA=1
Обозначим пропорции для разных сторон как: АМ=2х, 5х, а АВ как 3у, 4у
АМ=5х; АР=3х; ВР=4х
АС=4=2х.
2х=4
х=4÷2=2; х=2
АМ=5×2=10; АМ=10
Составим уравнение по стороне АВ:
3у+4у=8
7у=8
у=8/7
АР=3у=3×8/7=24/7;. АР=24/7
Найдём РМ, используя теорему косинусов: РМ²=АР²+АМ²-2×АР×АМ×cosA=
=(24/7)²+10²-2×24/7×1=
(576/49)+100-(480/7)= здесь находим общий знаменатель и получаем:
(576/49)+(4900/49)-(3360/49)=
=2116/49; РМ=√2116/49=46/7
или 6 целых 4/7
Построим ромб, нормаль ОК, и отрезки КА, КВ, КС, КД.
Рассмотрим прямоугольный ΔКОД. В нем известен катет ОК=8см, катет ОД=ВД/2=3 см (по свойствам диагоналей ромба, точкой пересечения они делятся пополам). Найдем гипотенузу КД=√(64+9)=√73 см.
КД=КВ=√73 см.
Рассмотрим прямоугольный ΔАОД (диагонали ромба пересекаются под прямым углом). В нем известен катет ОД=3 см, гипотенуза АД=5 см. Найдем катет АО=√(25-9)=√16 =4см.
АО в свою очередь является катетом в прямоугольном ΔАОК, где известен второй катет КО=8 см. Найдем гипотенузу КА=√(64+16)=√80
4√5 см.
КА=КС=4√5 см.
ответ: расстояния от точки К до вершин ромба КД=КВ=√73 см, КА=КС=4√5 см.

С=180-60-45=75
ВС/sin60=BD/sin75 BD=2sin75=1.93
ВС/sin60=CD/sin45 CD=корень2