Дан ΔABC площадью 18 см² ; М-точка пересечения его медиан. Прямая, проходящая через точку A и параллельная прямой BC, пересекает прямую BM в точке K, а прямую CM в точке N. Прямые BK и AC пересекаются в точке L. Найдите площадь Δ MLN
Решение.
S(МСВ)=1/3*18=6 (см²) по свойству медиан о разбиении треугольника на 6 равновеликих.
1)ΔАКL=ΔBCL по стороне и 2-м прилежащим углам :AL=LC (ВL-медиана) , ∠1=∠2 как накрест лежащие при АК||ВС , АС-секущая ,∠АLK=∠CLB как вертикальные .
{Значит S(АКL)=S(BCL)=1/2*18=9 (cм²);
{Значит LK=BL
2)Пусть ML=x , тогда по т. о точке пересечения медиан ВМ=2х, BL=3x, LK=3x.
3) ΔMNK ~ ΔMCB по 2-м углам :∠3=∠4 как накрест лежащие , ∠NMK=∠CMB как вертикальные ⇒ отношение площадей равно к².
k=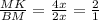 
⇒ S(MNK) : 6= 2² , S(MNK)=24
4) 
= 
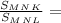
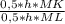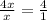
, S(MNL)= 6 cм²
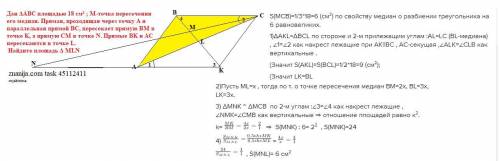
Даны точки A (-3;5) и B(4;2).
Примем координаты точки М(х; у).
Вектор АМ = ((х + 3); (у - 5)), вектор ВМ = ((х - 4); (у - 2)),
Длина АМ = √(((х + 3)² + (у - 5)²) = √(x² + 6x + 9 + y² - 10y + 25),
Длина BМ = √(((х - 4)² + (у - 2)²) = √(x² - 8x + 16 + y² - 4y + 4).
По условию задания:
3*√(x² + 6x + y² - 10y + 34) = √(x² - 8x + y² - 4y + 20).
Возведём в квадрат.
9*(x² + 6x + y² - 10y + 34) = x² - 8x + y² - 4y + 20.
9x² + 54x + 9y² - 90y + 306 = x² - 8x + y² - 4y + 20.
8x² + 62x + 8y² - 86y + 286 = 0.
Сократим на 8.
x² + (31/4)x + y² - (43/4)y + (143/4) = 0.
Выделим полные квадраты и получаем уравнение окружности:
(x + (31/8))² + (y - (43/8))² = 261/32.
Центр окружности О = (-31/8); (43/8)), радиус R = 2,855915.
1. Опустим перпендикуляр МО из точки М на плоскость α. Это и есть искомое расстояние. Треугольники АМО и ВМО прямлугольные, так как МО - перпендикуляр к плоскости α. АО=х, ВО=7х (дано). По Пифагору: в треугольнике АМО катет МО²=АМ²-АО² (1), в треугольнике ВМО катет МО²= ВМ²-ВО² (2). Приравняем (1) и (2): 144-х² = 576 - 49х² => 48х² = 432 => x² = 9. Подставим это значение в (1): МО²= 144-9=135. МО = √135 = 3√15 см.
ответ: расстояние от точки М до плоскости МО = 3√15 см.
2. Соединим точку М с вершинами правильного треугольника АВС. Получится правильная пирамида МАВС с вершиной в точке М. Точка М проецируется в центр О основания пирамиды (правильного треугольника), так как МА==МВ=МС (дано). Точка О является центром вписанной и описанной окружностей правильного треугольника (свойство). Радиус вписанной окружности, выраженный через сторону, равен r= (√3/6)*a, где "а" - сторона треугольника. В нашем случае r= МО =(√3/6)*12 = 2√3см. Радиус вписанной в треугольник окружности перпендикулярен к его сторонам, так как стороны являются касательными к вписанной окружности. По теореме о трех перпендикулярах отрезок МН также перпендикулярен этой стороне, то есть МН - искомое расстояние от точки М до стороны (любой) треугольника (его апофема). По Пифагору из треугольника МОН имеем МН=√(МО²+ОН²) = √(36+12) =4√3см.
ответ: искомое расстояние от точки М до сторон треугольника равно 4√3см.
3. В правильном треугольнике стороны равны. Расстояние от точки М до стороны ВС треугольника - это перпендикуляр МН из точки М к стороне ВС. По теореме о трех перпендикулярах основание Н высоты правильного треугольника АВС, опущенной из вершины А на сторону ВС и оснрвание перпендикуляра МН - это одна и та же точка. Следовательно, искомое расстояние МН можно найти по Пифагору из прямоугольного треугольника АМН,как гипотенузу, зная, что катет МА=2см(дано), а катет АН (высота правильного треугольника АВС) по формуле равен АН=(√3/2)*АВ=(√3/2)*4=2√3см. МН = √(МА²+АН²) = √(4+12) = 4см.
ответ: расстояние от точки М до стороны ВС равно 4см.