Сделай следующий рисунок: начерти треугольник АВС и впиши в него окружность. надо помнить, что центром окружности, вписанной в треугольник является точка пересечения биссектрис. Надо найти углы АОВ, АОС, ВОС.
Сначала найдем углы треугольника.
пусть х град. - величина одной части угла.
Тогда угол А= 3х град. угол В = 7х град, угол С = равен 8х град.
сумма углов треугольника равна 180 град. Составим и решим уравнение:
3х+7х+8х = 180
18х=180
х=10
10 градусов - величина одной части угла.
угол А=3*10 = 30 град
угол В=7*10=70 град.
угол С = 8*10 = 80 град.
Т.к АО и ОВ - биссектрисы углов А и В, то угол ВАО=15 град, угол АВО= 35 град., а их сумма равна 15+35=50 (град.), следовательно угол АОВ = 180 - 50 = 130(град)
ВО и СО - биссектриссы углов В и С, угол ОВС=35 град., угол ОСВ = 40 град., тогда их сумма равна 75 град. и следовательно угол ВОС = 180 - 75 = 105(град)
Тогда угол АОС можно вычислить так: 360 - (130+105) = 125(град).
ответ: угол АОВ= 130 град., угол ВОС = 105 град., угол АОС = 125 град.
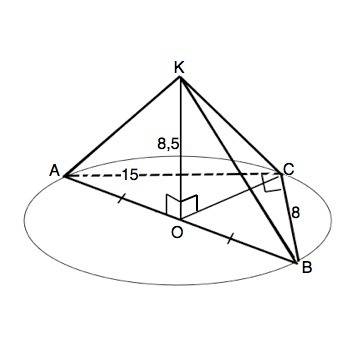
По т.Пифагора гипотенуза ∆ АВС
АВ=√(AC²+BC²)=√(225+64)=17 см.
Тогда АО=ОВ=8,5 см,
СО - медиана ∆ АВС, и равен половине гипотенузы по свойству медианы прямоугольного треугольника. СО= 8,5 см
КО ⊥ плоскости ∆ АВС, проекции наклонных АК, ВК, СК равны, ⇒ равны и сами эти наклонные.
В прямоугольных ∆ АКО, ∆ ВКО и Δ СКО катеты равны, ⇒ эти треугольники равные равнобедренные.
Острые углы равнобедренных прямоугольных треугольников равны 45° , ⇒
углы между плоскостью ∆ АВС и наклонными АК, ВК и СК равны 45°.
Параллелограмм MNPK: MN||PK, MP||NK, NK - диагональ.
MN + NK = 5:2 = 2.5 (см) - полупериметр параллелограмма
NK = Р треугольника - (MN+NK) = 4-2,5 = 1,5 (см)