1)периметр прямоугольника равен 24, а площадь 20. найдите большую сторону прямоугольника 2)периметр прямоугольника равен 44, а площадь 96. найдите большую сторону прямоугольника

👇

Ответ:

2005g6224

01.02.2020

P = 2(a + b), где а и b - стороны прямоугольника
S = ab

2(a + b) = 24
ab = 20 это система уравнений.

a + b = 12
ab = 20

b = 12 - a
a(12 - a) = 20 решим второе уравнение:

a² - 12a + 20 = 0
По теореме, обратной теореме Виета:
a₁ = 10
a₂ = 2

а = 10 a = 2
b = 2 b = 10

Большая сторона: 10

2.
P = 2(a + b), где а и b - стороны прямоугольника
S = ab

2(a + b) = 44
ab = 96 это система уравнений.

a + b = 22
ab = 96

b = 22 - a
a(22 - a) = 96 решим второе уравнение:

a² - 22a + 96 = 0
По теореме, обратной теореме Виета:
a₁ = 16
a₂ = 6

а = 16 a = 6
b = 6 b = 16

Большая сторона: 16

4,5(49 оценок)

Открыть все ответы

Ответ:

777alisham

01.02.2020

Обозначения:

R — радиус описанной окружности;

r — радиус вписанной окружности;

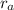r_a — радиус вневписанной окружности, соответствующей стороне ;

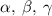$\alpha, \: \beta, \: \gamma$ — углы, противолежащие сторонам a, b и c соответственно;

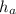h_a — высота, соответствующая стороне a.

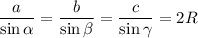$\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{ \sin \gamma}=2R$ — теорема синусов.

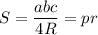$S=\dfrac{abc}{4R}=pr$ — формулы площади треугольника.

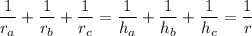$\dfrac{1}{r_a}+\dfrac{1}{r_b}+\dfrac{1}{r_c}=\dfrac{1}{h_a}+\dfrac{1}{h_b}+\dfrac{1}{h_c}=\dfrac{1}{r}$ — связь между радиусами вневписанных окружностей, длинами высот и радиусом вписанной окружности.

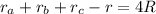
r_a+r_b+r_c-r=4R

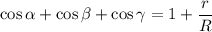
$\cos \alpha + \cos \beta + \cos \gamma=1+ \dfrac{r}{R}$

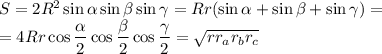
$S=2R^2 \sin \alpha \sin \beta \sin \gamma=Rr(\sin \alpha + \sin \beta + \sin \gamma)=\\ =4Rr \cos \dfrac{\alpha}{2} \cos \dfrac{\beta}{2} \cos \dfrac{\gamma}{2}=\sqrt{rr_ar_br_c$

— менее известные формулы площади треугольника.

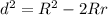d^2=R^2-2Rr — формула Эйлера, где d — расстояние между центрами вписанной и описанной окружностей.

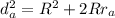d_a^2=R^2+2Rr_a — аналог формулы Эйлера для вычисления расстояния между центрами вневписанной (соответствующей стороне a) и описанной окружностей.

***

Этого хватит? Ведь записать «все» формулы невозможно: комбинируя имеющиеся формулы и находя новые зависимости, можно создать практически бесконечный список.

4,5(42 оценок)

Ответ: