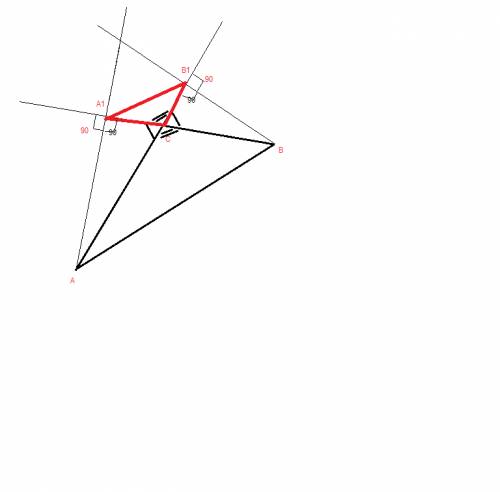
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
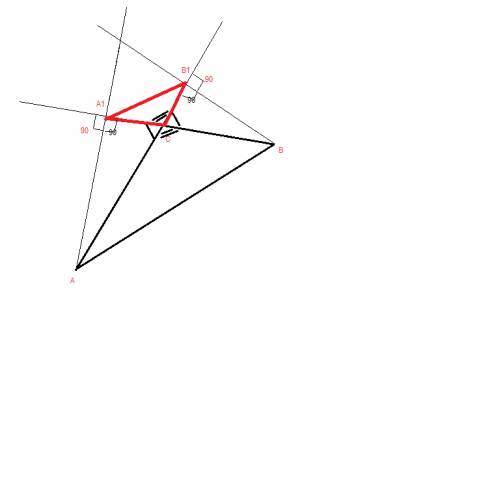
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
ответ: 192 см²
Объяснение:
У куба все грани квадраты. Диагонали квадрата равны и точкой пересечения делятся пополам.
Пусть О - точка пересечения диагоналей грани ABCD.
В треугольнике АВ₁С проведем отрезок ТО.
ТО - средняя линия треугольника АВ₁С, значит ТО ║ АВ₁,
т.е. ТО - это отрезок прямой k, проходящей через точку Т параллельно прямой АВ₁, расположенный внутри куба.
АВ₁ = 2ТО = 2 · 4 = 8 см по свойству средней линии.
Площадь квадрата можно найти как половину квадрата его диагонали (квадрат - ромб с равными диагоналями, а площадь ромба равна половине произведения его диагоналей):
Saa₁b₁b = 1/2 AB₁² = 1/2 · 64 = 32 см²
Площадь поверхности куба:
Sпов = 6 · Saa₁b₁b = 6 · 32 = 192 см²