Дано:
АВСА1В1С1 - прямая призма
АВ = 3 см
АС = 8 см
АА1 = 15 см - высота призмы
Найти:
S(бок) , S(полн) , V.
Решение.
Запишем уравнение теоремы косинусов
a^2 = b^2 + c^2 + 2bc*cos(a)
Рассмотри треушольник АВС. По теореме косинусов имеем
ВС^2 = AC^2 + AB^2 - 2*AC*AB*cos(60) =
= 8^2 + 3^2 - 2*8*3*0,5 =
= 64 + 9 - 24 =
= 49
тогда ВС = 7 см
Площадь боковой поверхности S(бок) прямой призмы
S(бок) = АА1*(АВ + АС + ВС) =
= 15(3 + 8 + 7) =
= 270 см^2
Найдем площадь основания S(осн) как площадь треугольника по двум сторонам и синус угла между ними
S(осн) = 0,5*АВ*АС*sin(60) =
= 0.5*3*8*кор (3)/2 =
= 6*кор (3) см^2
Полщадь полной поверхности S(полн) прямой призмы
S(полн) = S(бок) + S(осн) =
= 270 + 6*кор (3) см^2
Объем V прямой призмы
V = S(осн) *h =
= 6*кор (3)*15 =
= 90*кор (3) см^3
ответ: S(бок) = 270 см^2, S(полн) = 270 + 6*кор (3) см^2, V = 90*кор (3) см^3.
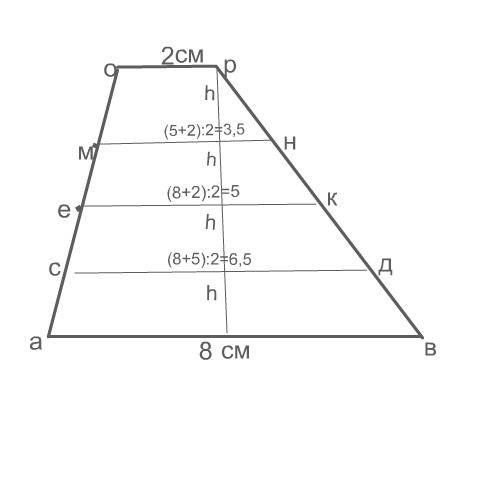
Обозначим концы отрезков, как указано на рисунке.
Вычислим длину каждого отрезка и площадь каждой получившейся трапеции
Длины отрезков обозначены в рисунке.
Они и основания, и средние линии между двумя основаниями бóльших трапеций.
S асдв=h(6,5+8):2=0,5h·14,5
S секд= h(5+6,5):2=0,5 h·11,5
S емнк=h((5+3,5):2=0,5h·8,5
S морн=h(3,5+2):2=0,5h·5,5
Сумма площадей трех верхних трапеций
S сорв =3h·8,5:2=h·12,75
площадь нижней -
S асдв = h·14,5:2=h·7,25
S сорв > S асдв
---------------------------------
Что касается этого: в) Укажите какие-нибудь значения оснований (вместо чисел 2 и 16), чтобы ответом на пункт б) было словосочетание «они равны» - надо подумать.
Возможно, ошибаюсь, но думаю, что при таком делении трапеции таких сторон не найти.
AR/AB = RC/BC
AR/AB = (AC - AR)/BC
AR = 35/11; RC = 42/11
AP/AC = (AB - AP)/BC
AP = 35/13; BP = AB - AP = 30/13
BQ/AB = (BC - BQ)/AC
BQ = 5/2; QC = BC - BQ = 7/2
S = S(ABC) = 6√6 (по формуле Герона)
S(PQR) = S - S(APR) - S(PBQ) - S(RQC)
S(ABC)/S(APR) = (AB·AC)/(AP·AR) (если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы)
S(APR) = S(ABC)·AP·AR/(AB·AC) = S·35/143
аналогично находятся S(RQC) = S·7/22 и S(PBQ) = S·5/26
S(PQR) = (210√6)/143