Дана правильная треугольная пирамида abcd, сторона основания и высота которой равна 6√3 и 4 соответственно. найдите угол между прямой ef и плоскостью основания abc, если f - середина ребра db, a e лежит на ad так, что ae: ed=3: 1.

👇

Увидеть ответ

Ответ:

abdualieva130403

11.08.2022

Находим проекции боковых рёбер на основание.

Они равны (2/3) высоты основания,то есть (2/3)*(6√3*(√3/2)) = 6.

Проекции точек E и F отделяют на основании отрезки от основания высоты, равные (1/4)*6 = 3/2 и (1/2)*6 = 3.

Получаем проекцию E1F1 отрезка EF на основание как сторону треугольника с двумя известными сторонами (3/2) и 3 и углом между ними 120 градусов.

E1F1 = √((9/4) + 9 - 2*(3/2)*3*cos120°) = √(9 +36 + 18)/2 = √63/2.

Высоты точек E и F от основания равны соответственно (3/4)*4 = 3 и (1/2)*4=2. Разность высот равна 3 - 2 = 1.

Угол между прямой EF и плоскостью основания ABC - это плоский угол между прямыми EF и E1F1.

Отсюда находим тангенс искомого угла.

tg α = 1/(√63/2) = 2/√63 ≈ 0,251976.

Угол α = 0,24684 радиан или 14,14277 градуса.

4,6(2 оценок)

Открыть все ответы

Ответ:

kristinasotsen

11.08.2022

№1

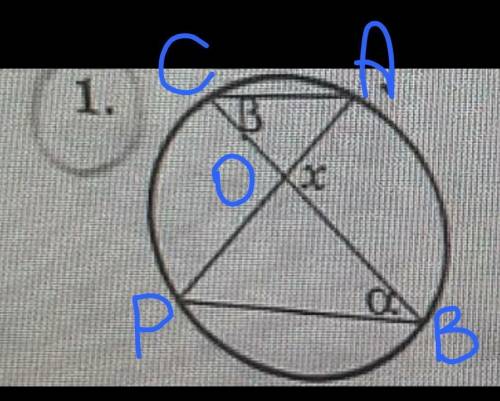
Дано:

Угол АСВ=34°;

Угол СВР=18°;

Найти: угол АОВ.

Углы АСВ и АРВ – вписанные и опираются на одну и ту же дугу АВ, следовательно угол АРВ=угол АСВ=34°.

Сумма углов в любом треугольнике равна 180°.

Тогда угол ВОР=180°–угол ОРВ–угол ОВР=180°–34°–18°=128°.

Углы ВОР и АОВ – смежные, значит в сумме дают 180°.

Тогда угол АОВ=180°–угол ВОР=180°–128°=52°.

ответ: 52°

№2

Дано:

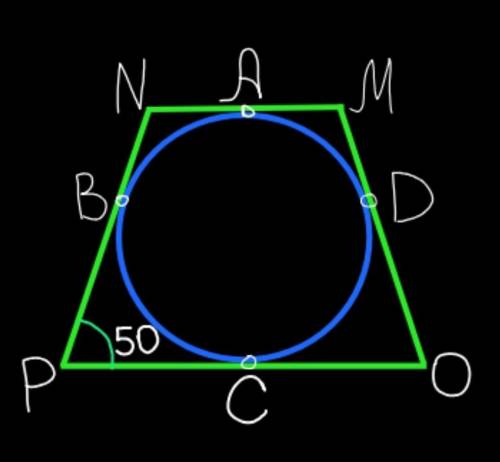
РNMO – равнобедренная трапеция, описанная вокруг окружности;

Точки А, В, С, D – точки касания;

Угол NPO=50°.

Найти: дуги АВ, ВС, СD, AD.

Углы при боковой стороне трапеции в сумме равны 180°, тогда угол РNM=180°–угол NPO=180°–50°=130°.

Углы при основании равнобедренной трапеции равны, то есть угол МОР=угол NPO=50°; угол OMN=угол PNM=130°.

Угол между двумя касательными, проведёнными из одной точки, равен разности 180° и градусной меры меньшей дуги, заключённой между данными касательными.

То есть:

Угол NPO=180°–дуга ВС => дуга ВС=180°–угол NPO=180°–50°=130°;

Угол МОР=180°–дуга CD => дуга CD=180°–угол МОР=180°–50°=130°;

Угол РNM=180°–дуга АВ => дуга АВ=180°–угол PNM=180°–130°=50°;

Угол OMN=180°–дуга AD => дуга AD=180°–угол OMN=180°–130°=50°.

ответ: 50°; 50°; 130°; 130°.

Геометрия 8 класс a=18b=34за данными малюнка знайдіть кут х2.Коло доторкається до сторін рівнобндерн

4,6(75 оценок)

Ответ:

ainurka88akgmailcom

11.08.2022

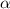#1. l-длина дуги, S- площадь сектора, $\alpha$ - градусная мера сектора, R- радиус окружности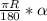
l= $\frac{ \pi R}{180} * \alpha$
Подставим известное и получим
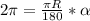
$2 \pi = \frac{ \pi R}{180} * \alpha$
Выразим R и получим
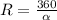
$R= \frac{360}{ \alpha }$
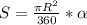
$S= \frac{ \pi R^{2} }{360} * \alpha$
Подставим известное
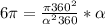
$6 \pi = \frac{ \pi 360^{2} }{ \alpha ^{2} 360} * \alpha$
Отсюда
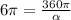
$6 \pi = \frac{360 \pi }{ \alpha }$
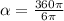
$\alpha = \frac{360 \pi }{6 \pi }$
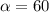
$\alpha =60$
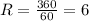
$R= \frac{360}{60} = 6$
ответ : 6 см, 60°.
#2. Дано: d впис= 10 см, a(сторона многоугольника) = 10√3
Найти: n(кол-во сторон), R опис
Решение: r(радиус впис окр)=0.5d=5см
Выразим радиус описанной окружности через сторону и через радиус вписанной окружности, а затем приравняем
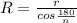
$R= \frac{r}{cos \frac{180}{n}}$
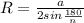
$R= \frac{a}{2sin \frac{180}{n} }$
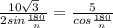
$\frac{10 \sqrt{3} }{2sin \frac{180}{n} } = \frac{5}{cos \frac{180}{n} }$
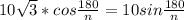
$10 \sqrt3*cos \frac{180}{n} = 10sin \frac{180}{n}$
Сокращаем на 10 и получаем
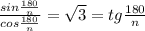
$\frac{sin \frac{180}{n} }{cos \frac{180}{n} } = \sqrt{3} = tg \frac{180}{n}$
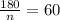Тангенс, равный √3 имеет угол в 60°, а значит, $\frac{180}{n} =60$ , откуда n=3
Так как многоугольник- треугольник, то радиус вписанной окружности равен половине радиуса описанной., значит, R=2r=10см
ответ: 3 стороны, 10 см.

4,4(47 оценок)

Это интересно:

Хобби-и-рукоделие

26.07.2020

Как выращивать спирулину дома...

26.01.2022

Как помочь другу справиться с депрессией...

Дом-и-сад

28.11.2021

Как сделать небольшую септическую систему...

Здоровье

16.08.2022