Вариант 1
№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC = 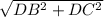 =
= 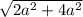 =
= 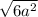 =
= 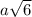
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 = 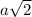
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
DB = DC = BC = 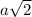
(Дальше долко)
Периметр ABK P=AB+BK+AK;
Периметр ABC=AB+AC+BC=AB+AK+KB+BC=2AB+2AK=2(AB+AK)=2(Pabk-BK)=2(16-5)=2*11=22 см
Задача 2
Т.к. AB=BC, AF=EC=AB/2=BC/2;
Рассмотрим треугольники AFC и CEA
Они равны по двум сторонам (AF=EC и AC - общая) и углу между ними (EAC=FCA)
Тогда углы EAC=FCA.
Значит, угол BAE=BAC-EAC=BCF
Углы FMA=EMC, как вертикальые
Тогда углы AFM=180-FMA-FAM=MEC
Значит, треугольники AFM=EMC по стороне (EC=AF) и двум прилежащим к ней углам (AFM=MEC и FAM=ECM)
Тогда AM=MC => треугольник AMC - равнобедренный