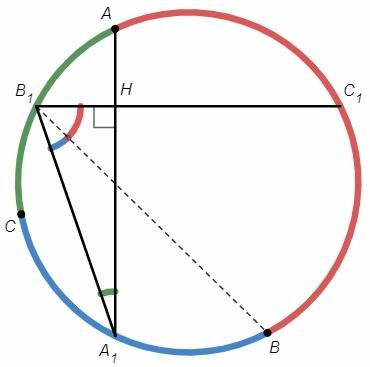
Вершины △ABC разбивают описанную окружность на три дуги. Биссектрисы углов треугольника делят эти дуги пополам (два равных вписанных угла опираются на равные дуги), точки A1, B1, C1 - середины дуг.
Вписанные углы ∠BB1C1, ∠BB1A1, ∠A1 опираются на половины дуг AB, BC, AC, следовательно сумма вписанных углов равна четверти окружности, 90.
∠BB1C1+∠BB1A1+∠A1 =∪AB/4+∪BC/4+∪AC/4 =360/4 =90
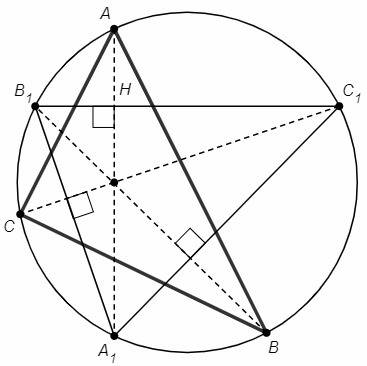
AA1 и B1C1 пересекаются в точке H. В △A1B1H сумма углов ∠A1 и ∠B1 равна 90, треугольник прямоугольный, AA1 и B1C1 пересекаются под прямым углом.
Аналогично BB1⊥A1C1, CC1⊥A1B1. Биссектрисы △ABC являются высотами △A1B1C1. Центр вписанной окружности (пересечение биссектрис) △ABC является ортоцентром (пересечением высот) △A1B1C1.
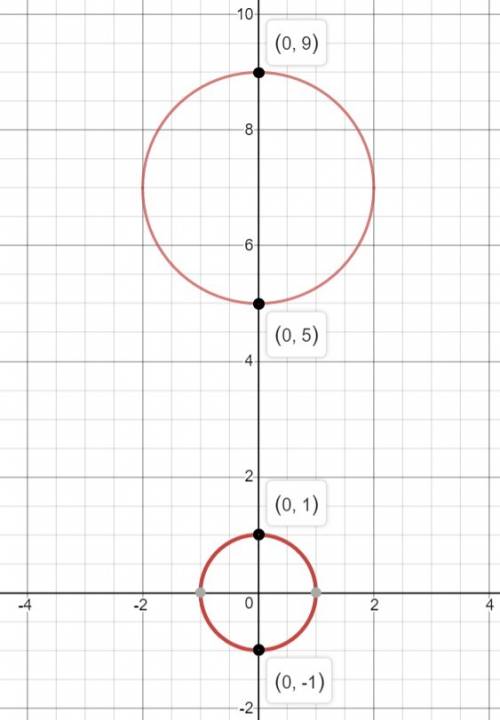
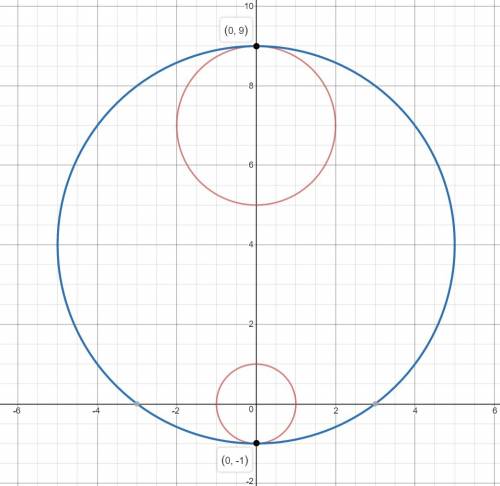
Окружность №1: x²+y²=1. Центр (0; 0), радиус 1.
Окружность №2: x²+(y-7)²=4. Центр (0; 7), радиус 2.
Для удобства и полного понимания ситуации строим данные окружности (изображение 1). Рассмотрим все возможные варианты:
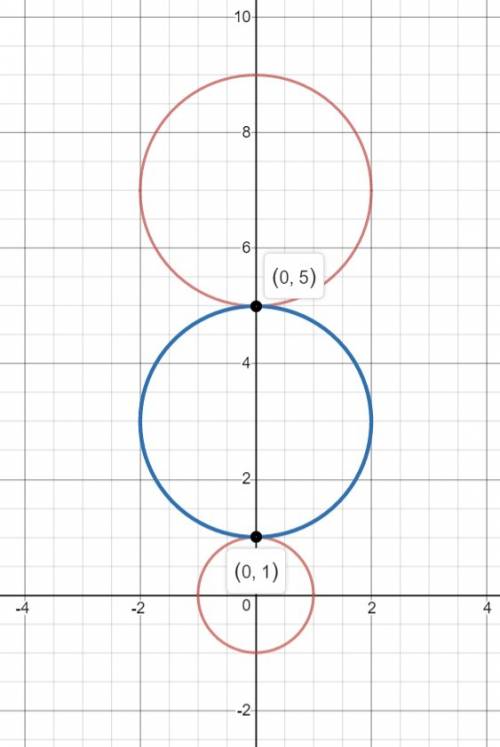
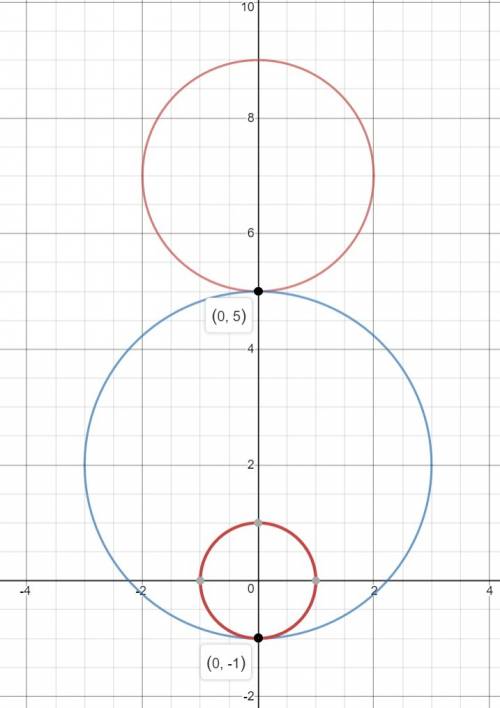
1) Окружность касается обоих данных окружностей внешним образом (изображение 2). В таком случае ее центр (0; 3), радиус 2.
x²+(y-3)²=4
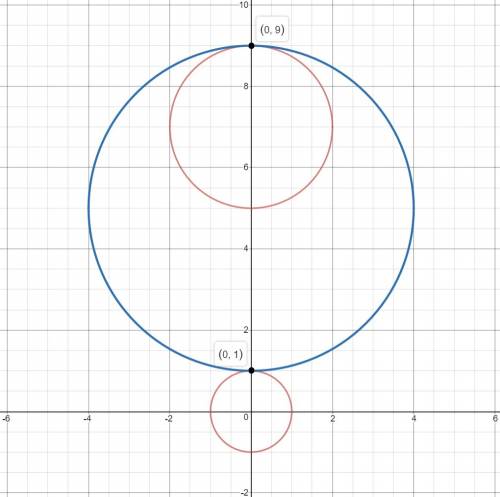
2) Окружность касается обоих данных окружностей внутренним образом (изображение 3). В таком случаем ее центр (0; 4), радиус 5.
x²+(y-4)²=25
3) Окружность касается первой окружности внутренним образом, второй внешним (изображение 4). В таком случае ее центр (0; 2), радиус 3.
x²+(y-2)²=9
4) Окружность касается первой окружности внешним образом, второй внутренним (изображение 5). В таком случае ее центр (0; 5), радиус 4.
x²+(y-5)²=16
синус это отношение противолежащего катета к гипотенузе, сосинус это отношение прилежащего катета к гипотенузе, тангенс это отношение противолежащего катета к прилежащему, ну а котангенс функция обратная тангенсу. тут есть два хода решения, так как у данного треугольника и угол В и угол А будут острыми, я делаю расчет на угол А.
Синус А равен 21/29, Сосинус А равен 20/29, Тангенс А равен 21/20, ну и Котангентс равен 20/21