Пересчение двух прямых отличной от развернутого называется вертикальным.
Противоположные углы вертикальных углов равны.
Соседние углы вертикальных углов являются смежными.
Сумма смежных углов 180 градусов.
Зная эти теоремы решим задачу.
Пусть значение градусных мер будет х. Тогда один из углов 4х, а другой 5х. Т.к. эти углы смежные, тогда сумма их составляет 180 градусов. Тогда создадим уравнение и решим:
4х + 5х = 180
9х = 180
х = 20 значение град. мер.
20 * 4 = 80 градусов один из углов.
20 * 5 = 100 град. другой угол.
ответ: 80 град., 100 град.
AD = 15 см.
Объяснение:
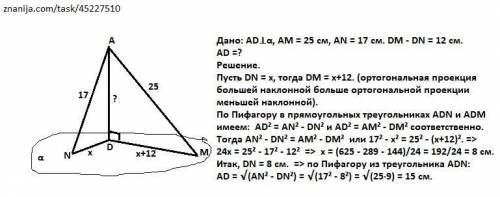
Дано: AD⊥α, AN = 17 см. AM = 25 см. DM - DN = 12 см.
Найти AD.
Решение.
Пусть DN = x, тогда DM = х+12. (ортогональная проекция большей наклонной больше ортогональной проекции меньшей наклонной).
По Пифагору в прямоугольных треугольниках ADN и ADM имеем: AD² = AN² - DN² и AD² = AM² - DM² соответственно.
Тогда AN² - DN² = AM² - DM² или 17² - х² = 25² - (х+12)². =>
24х = 25² - 17² - 12² => х = (625 - 289 - 144)/24 = 192/24 = 8 см.
Итак, DN = 8 см. => по Пифагору из треугольника ADN:
AD = √(AN² - DN²) = √(17² - 8²) = √(25·9) = 15 см.
12см расстояние от точки до плоскости треугольника.
Объяснение:
а=8см основание треугольника
h=8см высота треугольника
с=13см расстояние от точки до вершин треугольника
b=? боковая сторона треугольника
S∆=? площадь треугольника
R=? радиус описанной окружности вокруг треугольника
Н=? расстояние от точки к плоскости треугольника
S∆=1/2*a*h=1/2*8*8=32см площадь треугольника.
Высота равнобедренного треугольника является медианой.
По теореме Пифагора найдем боковую сторону треугольника.
b=√((a/2)²+h²)=√((8/2)²+8²)=√(16+64)=√80=
=4√5см боковая сторона треугольника
R=(a*b*b)/4S∆=(8*4√5*4√5)/(4*32)=
=640/128=5см радиус описанной окружности
Теорема Пифагора
с=13см ребро пирамиды
Н=√(с²-R²)=√(13²-5²)=√(169-25)=12см высота пирамиды
4x+5x=180
9x=180
x=180/9
x=20
4x=4*20=80
5x=5*20=100
ответ: 80, 100,80,100 градусов.