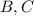отрезки 
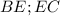, где точка 
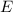пересечение с окружностью. Обозначим точку перпендикуляра 
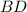с 
. 
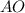
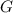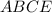, который вписан в окружность. 
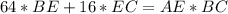, так как 
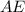лежит на центре , то треугольники 
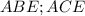прямоугольные. 
. 
. 
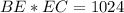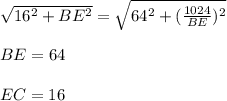
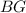- высота прямоугольного треугольника 
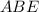, тогда 
.
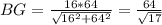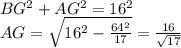, так как 
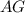является высотой прямоугольного треугольника 
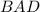, то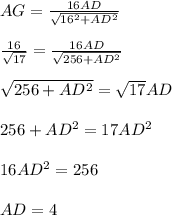 
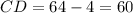
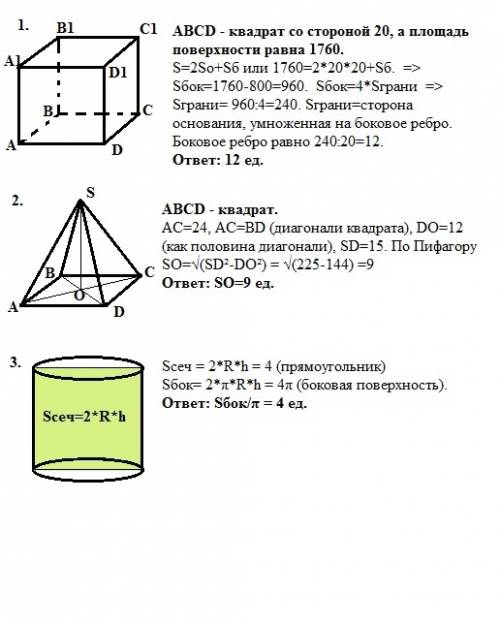
1. ABCD - квадрат со стороной 20, а площадь поверхности призмы равна 1760. Sп=2So+Sб или 1760=2*20*20+Sб. => Sбок=1760-800=960. Sбок=4*Sграни => Sграни= 960:4=240. Sграни=сторона основания, умноженная на боковое ребро. Боковое ребро равно 240:20=12.
ответ: 12 ед.
2. ABCD - квадрат. АС=24, АС=BD (диагонали квадрата), DO=12 (как половина диагонали), SD=15. По Пифагору SO=√(SD²-DO²)=√(225-144) =√81 = 9 ед.
ответ: SO=9 ед.
3. Sсеч = 2*R*h = 4 (прямоугольник). Sбок= 2*π*R*h = 4π (боковая поверхность).
ответ: Sбок/π = 4 ед.
Площадь основания найдем по формуле Герона: S=√[p(p-a)(p-b)(p-c)], где р - полупериметр, а,b, и с - стороны треугольника. S=√(16*6*6*4)=48.
Радиус вписанной окружности найдем из формулы: S=p*r: r=S/p.
В нашем случае r=48/16=3.
Высоту пирамиды найдем из прямоугольного треугольника, образованного высотой пирамиды, радиусом вписанной окружности (катеты) и высотой грани. Острые углы этого треугольника равны 45° (дано), значит высота пирамиды равна радиусу.
Тогда V=(1/3)So*h или V=(1/3)48*3=48.