5
Объяснение:
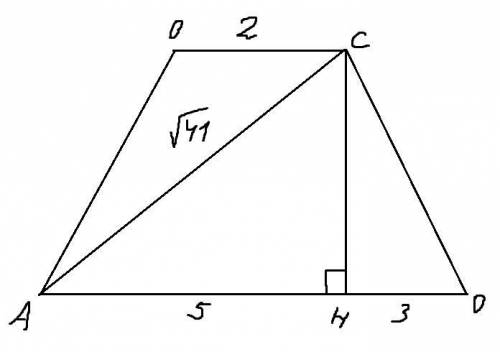
Из точки С опустим перпендикуляр СН на основание AD. Тогда по теореме Пифагора CH = √AC²-AH² = √41 - 25 = √16 = 4. В прям. треугольнике CHD HD = 3, CH = 4. Тогда по теореме Пифагора боковая сторона CD = √4² + 3² = √16+9 = √25 = 5
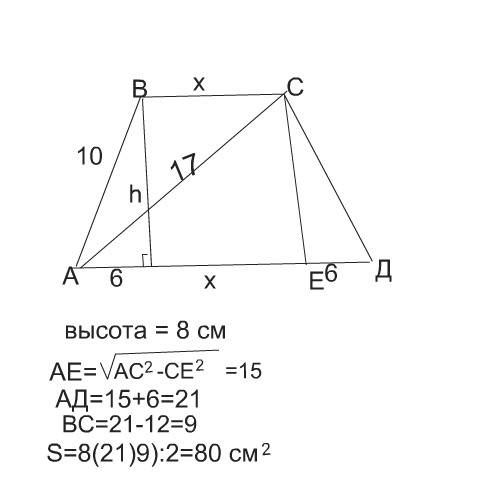
В параллелограмме, тупой угол которого равен 150°, острый равен 180-150=30°
Биссектриса делит тупой угол пополам, следовательно, угол при пересечении ее со стороной, к которой она проведена,тоже равен ее половине ( сумма углов треугольника, так же, как сумма углов параллелограмма при одной стороне, равна 180°).
Благодаря биссектрисе получился равнобедренный треугольник с углами при основании, равными 75° ( это значения здесь не имеет) и сторонами 16 см.
Меньшая сторона параллелограмма равна 16 см, высота, которую мы проведем из вершины тупого угла к большей стороне, равна половине от 16,т.к. противолежит углу 30°.
Имеем все данные для вычисления площади параллелограмма:
высота 8 см
основание 16+5=21 см
S=8·21= 168 см²
-----------------
2..
Площадь треугольника равна половине произведения высоты на основание, к которому она проведена.
Высота
h=7√2*sin (45º)=7√2* √2:2=7*2:2=7см
Основание =10 см
S=19*7:2=35 cм²
-------------------------------------------
Третья задача - в рисунке, ничего сложного там нет - разберетесь.
Если опустить высоты из вершин тупых углов, то большее основание
8= 2+2х, х=3 где х- отрезки, большего основания, заключенные между вершинами трапеции и основаниями этих высот. Тогда по теореме Пифагора высота равна √((√41)²-(3+2)²)=√(41-25)=4/см/