Sполн = 50+100√7 см².
Объяснение:
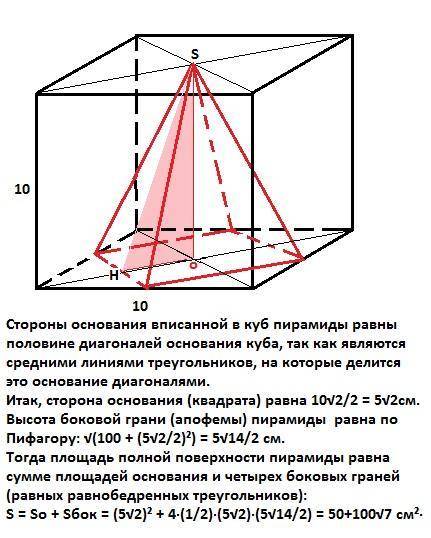
Стороны основания вписанной в куб пирамиды равны половине диагоналей основания куба, так как являются средними линиями треугольников, на которые делится это основание диагоналями.
Итак, сторона основания (квадрата) равна 10√2/2 = 5√2 см.
Высота боковой грани (апофемы) пирамиды равна по Пифагору:
√(100 + (5√2/2)²) = 5√14/2 см.
Тогда площадь полной поверхности пирамиды равна сумме площадей основания и четырех боковых граней (равных равнобедренных треугольников):
S = So + Sбок = (5√2)² + 4·(1/2)·(5√2)·(5√14/2) = 50+100√7 см²·
Треугольник abc - равнобедренный,(т.к. угол с =90,а угол а=45,след.в=45 по сумме углов треугольника),означает bс=ас
Гипотенуза одинакова 8,по аксиоме пифагора сумма квадратов катетов равна 64(8 в квадрате),след. катет равен корню из 32
bm-медиана,потому мс=0,5ас;
рассмотрим треугольник bcm: угол с равен 90,мс=0,5ас,bc=корню из 32
по теореме пифагора в новеньком треугольнике ищем гипотенузу(bm):
гипотенуза=корень из((корень из 32) в квадрате+(корень из 32,деленный на два)в квадрате=корень из 40=два корня из 10