94.
Если углы 1 и 2 равны, а они образованы прямой, пересекающей две другие, то прямые b и c параллельны.
Угол 2 равен углу 3. Углы 2 и 3 являются внешними накрест лежащими, а по теореме, если прямая, секущая две прямые, образует равные внешние накрест лежащие углы, то эти прямые параллельны. b||c, и b||a, следовательно, прямые a и c параллельны.
95.
По теореме, если Треугольники имеют равные две стороны и угол между ними, то эти Треугольники равные. Стороны AC и A1C1 соответственны и лежат на одной прямой, а также находятся над прямой, следовательно AB||A1B1.
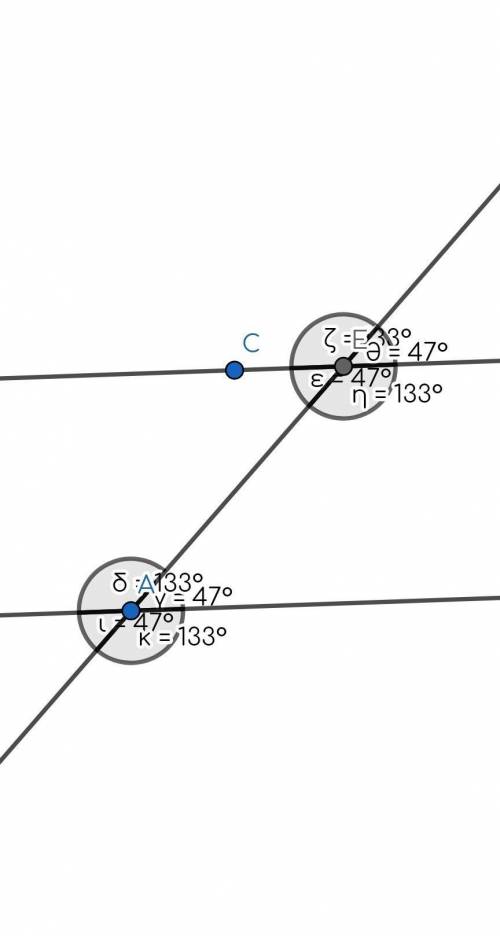
97. Картинка выше.
Все тупые углы - 133°
Все острые - 47°
Объяснение:
Независимо, если какие-то подобные, или соответственные стороны треугольников лежат на одной прямой и находятся в одной полуплоскости, то все подобные стороны параллельны.
Пусть дан равнобедренный треугольник АВС, АВ=ВС - боковые стороны, АС - основание, ВЕ - высота, биссектриса, медиана треугольника, АК делит сторону ВС в отношении 2:5, считая от вершины С, т.е. СК:КВ=2:5. Пусть ВЕ пересекается с АК в точке О.
Биссектриса треугольника обладает следующим свойством: биссектриса делит противолежащую сторону треугольника на отрезки пропорциональные двум другим сторонам.
ВЕ - биссектриса треугольника АВС и соответственно ВО - биссектриса треугольника АВК.
Пусть х - коэффициент пропорциональности, то СК=2х, КВ=5х, то ВС=АВ=7х. Значит ВО делит сторону АК в отношении 7:5 считая от вершины А, т.е. АО:ОК=7:5
х(м)=(х(а)+∧х(в))/(∧+1) х(м)=(-2+1/2*4)/1+1/2=(-2+2)/(3/2)=0
у(м)=(у(а)+∧у(в))/(∧+1) у(м)=(5+1/2*(-3))/1+1/2=(5-3/2)/(3/2)=7/2*2/3=7/3
М(0;7/3)
2) Если точка М принадлежит прямой АВ, то возможны 2 варианта: первый рассмотрен под цифрой 1), а второй т.А будет серединой отрезка МВ, тогда х(м) и у(м) можно найти из формул середины отрезка
х(а)=х(м)+х(в)/2 -2=(х(м)+4)/2 х(м)=(-2*2)-4=-8
у(а)=у(м)+у(в)/2 5=(у(м)-3)/2 у(м)=5*2+3=13
М(-8;13)
3)(х(м)-х(а))²+(у(м)-у(а))²=100 и (х(м)-х(в))²+(у(м)-у(в))²=100
для удобства заменим х(м) на х, а у(м) на у, получим уравнения
(х+2)²+(у-5)²=100 х²+4х+4+у²-10у+25=100
(х-4)²+(у+3)²=100 х²-8х+14+у²+6у+9=100
вычтем уравнения 12х-16у+16=0 3х-4у=-4 у=3/4х+1
подставим в первое уравнение (х+2)²+(3/4х-4)²=100
х²+4х+4+9/16х²-6х+16=100
25/16х²-2х-80=0
Д1=1+25/16*80=1+25*5=126=3√14
х1=(1+3√14)/(25/16)=16(1+3√14)/25 и х2=16(1-3√14)/25
у1=3/4*16*(1+3√14)/25+1=12(1+3√14)/25+1=(37+36√14)/25
у2=3/4*16*(1-3√14)/25+1=(37-36√14)/25
(16(1+3√14)/25;(37+36√14)/25) (16(1-3√14)/25;(37-36√14)/25)
4) (х-х(а))²+(у-у(а))²+(х-х(в))²+(у-у(в))²=50
(х+2)²+(у-5)²+(х-4)²+(у+3)²=50
х²+4х+4+у²-10у+25+х²-8х+16+у²+6у+9=50
2х²-4х+2у²-4у+54=50
х²-2х+1+у²-2у+1+25=25
(х-1)²+(у-1)²=0
точка М(1;1)