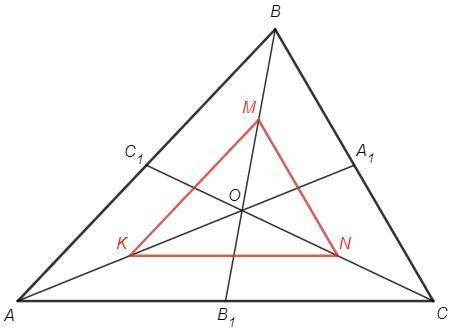
Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
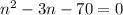
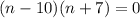
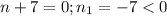- не подходит, количество вершин не может быть отрицательным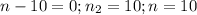
r= =2⇒ 2= ⇒ АВ=17-4=13
2 2
АС²+ВС²=13²=169
АС=17-ВС
289-34ВС+ВС²+ВС²=169
120-34ВС+2BC²=0
D=1156-960=196
BC=(34+-14)/4=5
AC=17-5=12
Площадь прямоугольного треугольника = АС*ВС/2
S=12*5/2=30