Примем дугу ЕКН за х
Тогда дуга ЕАН=х+90
В сумме эти две дуги составляют 360 градусов.
х+х+90=360
2х=360-90
2х=270
х=135
х+90=135+90=225
Вписанный угол ЕАН опирается на дугу, равную 135 градусов. Он равен половине центрального угла, опирающегося на ту же дугу
135:2=67,5
Вписанный угол ЕКН опирается на дугу, равную 225 градусов.
Он равен половине центрального угла, опирающегося на ту же дугу и равен
225:2=112, 5
Вписанный угол ЕКА опирается на дугу 180 градусов, и равен половине центрального угла 180 градусов
180:2=90
угол ЕАН=67,5ᵒ
угол ЕКН=112, 5ᵒ
угол ЕКА=90ᵒ
ответ: l²=34
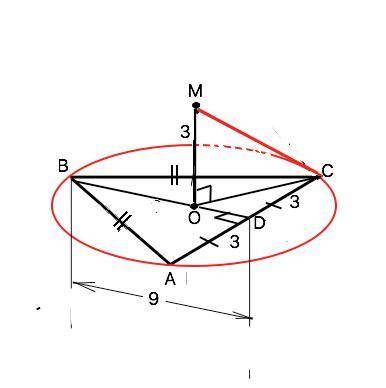
Объяснение: Точка M равноудалена от всех вершин данного треугольника, следовательно, все наклонные из М к вершинам, а, значит, и к плоскости треугольника, равны, поэтому равны и их проекции ОС=ОВ=ОА и равны радиусу описанной около ∆ АВС окружности.
Искомое расстояние МС - гипотенуза прямоугольного ⊿ МОС. Для её нахождения нужно найти катет ОС этого треугольника. ОС=R.
Формула радиуса описанной окружности R=a•b•c/4S ( где а, b и с - стороны треугольника).
S=BD•AC:2=9•6:2=27
Боковые стороны ∆ (АВС) найдём из ⊿ АВD. Высота ВD в равнобедренном треугольнике ещё и медиана (свойство)
По т.Пифагора. АВ=√(BD²+AD²)=√(9²+3²)=√90
R=(√90•√90•6):4•27= 5
ОС=5 ⇒ МС²=(MO²+OC²)=3²+5²=34 ⇒ l²=34
Дана равнобедренная трапеция ABCD.Линии при основании равны 6 см и 12 см.Угол при основании равен 60 градусам.Найти периметр и боковые стороны трапеции.
в трапеции опустим 2 перпендикуляра bb1 и cc1 угол при основании a он равен углу d так как равнобедренная трапеция ab=cd треугольник abb1=треуг сс1d по 2 признаку ( угол a=d, ab=dc ,2 угла равны так как они по 90 перпендикуляры) значит ab1=c1d=3 см ab=6 потаму что ab1 лежит против угла 30 градусов он равет половине гипотенузы (ab1=3 то ab=6) ab=cd=6 см Р abcd=6+6+6+12=30 ответ р=30 а стороны равны ab=6 см cd=6см