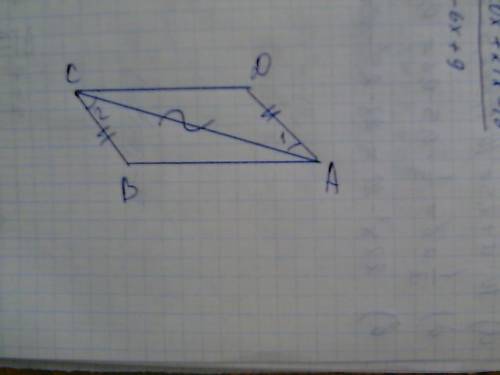
Как известно, диагонали точкой пересечения делятся пополам, а противоаоложные стороны пар-мма равны. Следовательно, противоположные по отношению друг к другу треугольники равны(по 3-ему признаку равенства треугольников), и площади их тоже равны.
Осталось доказать, что площади двух "смежных" треугольников равны. Рассмотрим их. Одна сторона у них общая, примем за основание сторону, лежащую на диагонали. Эти стороны у треугольников равны, т.к. точкой пересечения, повторюсь, диагонали делятся пополам. Прощадь треугольника у нас равна половине основания, умноженного на высоту, проведенную к основанию. Проведи к основаниям треугольников высоту - это будет один и тот же отрезок.
Мы получили - основания у треугольников равны, высоты равны.
Теорема доказана.
а)Сумма углов четырехугольника АВДС равна 360 градусов. Поэтому, чтобы найти угол АСД надо из 360 отнять сумму заданных углов. Т.е. угол ACD= 360-(43+45+ 137)=360-225=135 градусов. б)Угол BDC =45 градусам, ABD=137 градусам, это внутренние односторонние углы при прямых АВ и DC и секущей BD. Для того, чтобы прямые АВ и DC были параллельны, надо чтобы сумма указанных углов была 180 градусов, а у нас 45+ 137= 182, т.е. эти прямые не параллельны, значит, они имеют общую точку и, если АВ и DC продолжить, то они пересекутся.