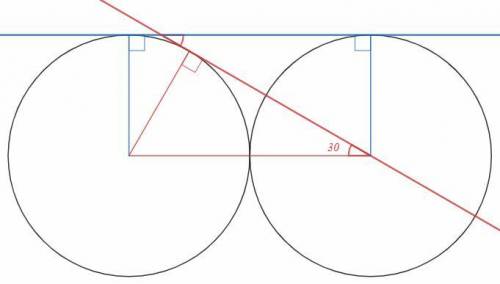
Прямая касается двух окружностей, точки касания удалены от центров на радиусы. Так как радиусы равны, точки касания равноудалены от центров и лежат на прямой, параллельной линии центров.
Окружности касаются внешним образом, точка касания лежит на линии центров, расстояние между центрами равно двум радиусам. Радиус, поведенный в точку касания, перпендикулярен касательной и образует прямоугольный треугольник, в котором линия центров - гипотенуза. Катет равен половине гипотенузы, значит он лежит против угла 30.
Искомый угол является накрест лежащим при параллельных и равен 30.
Пусть в равнобедренном Δ АВС угол С при вершине равен 24⁰ => углы при основании будут равны (180⁰ - 24⁰)/2 = 78⁰.
В другом равнобедренном Δ А₁В₁С₁ угол при основании равен 78⁰ , значит угол при вершине равен 180⁰ - 2*78⁰ = 180⁰ - 156⁰ = 24⁰.
Т.о. в трегольниках Δ АВС и Δ А₁В₁С₁ углы соответственно равны => по признаку подобия треугольников Δ АВС и Δ А₁В₁С₁ подобны.