См. Объяснение
Объяснение:
∠В треугольника АВС равен ∠АСD треугольника ACD - согласно условию (отмечены одинаковыми дужками);
∠ВСА треугольника АВС равен ∠САD треугольника ACD - так как, согласно условию, ADCD является трапецией, поэтому AD║ BC, и угол
∠ВСА = ∠САD как углы внутренние накрест лежащие при параллельных прямых AD║ BC и секущей АС.
Согласно первому признаку подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Что и требовалось доказать.
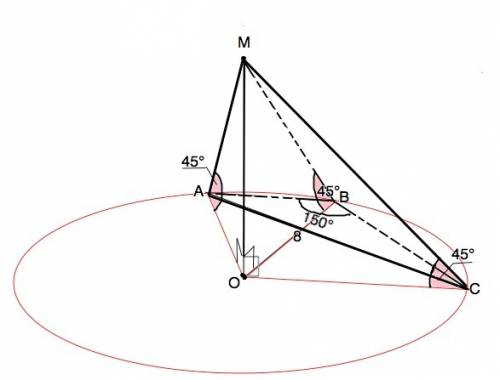
Обозначим основание пирамиды АВС, угол АВС=150°, высота пирамиды МО.
Боковые ребра наклонены к основанию под одинаковым углом, значит, их проекции равны между собой и равны радиусу описанной около основания окружности.
Треугольник АВС - тупоугольный. Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Так как угол наклона ребер равен 45°, то высота пирамиды является катетом равнобедренного треугольника и равна радиусу описанной окружности.
По т.синусов 2R=АС:sinАВС=
⇒ R=8 см
Высота МО пирамиды равна R=8 см
если 1=2, то это либо вертикальные углы, либо накрест лежащие... и они
равны 180-120=60..
а 3 и 4=120