вот так:
there are three rooms in my house
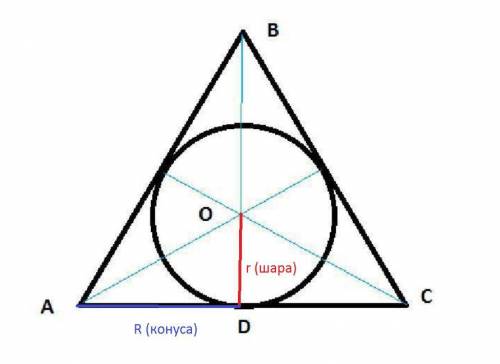
в доме я имею свою комнату. ,лучшее решение!Осевое сечение конуса – равнобедренный треугольник АВС.
АВ=ВС – образующие.
BD– высота конуса, а также высота, медиана и биссектриса равнобедренного треугольника.
О–центр вписанной в треугольник АВС окружности и центр вписанного в конус шара.
ОD=r .
AD=R .
Из прямоугольного треугольника
tg∠OAD = tg(α/2) = r/R . Отсюда r = Rtg(α/2).
ОА– биссектриса угла ВAD, так как центр вписанной в треугольник окружности– точка пересечения биссектрис.
Высота конуса H = R/tg(α/2).
V(шара) = (4/3)πr³ = (4/3)πR³tg³(α/2).
V(конуса)=(1/3)S(осн)·H=(1/3)·πR²·R/tg(α/2) = (1/3)·πR³/tg(α/2).
Разделим V(конуса) на V(шара).
V(конуса) / V(шара) = ( (1/3)·πR³/tg(α/2)) / ((4/3)πR³tg³(α/2)) = 4tg³(α/2)tgα.
ответ: V(конуса) = V(шара) / (4tg³(α/2)tgα).
На рисунке обозначены:
ABC - Основание пирамиды
OS - Высота
KS - Апофема
OK - радиус окружности, вписанной в основание
AO - радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO - двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)
Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).
Свойства правильной треугольной пирамиды:
боковые ребра правильной пирамиды равны
все боковые грани правильной пирамиды являются равнобедренными треугольниками
в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан
there are three rooms in my house