∠САВ=165°
Объяснение:
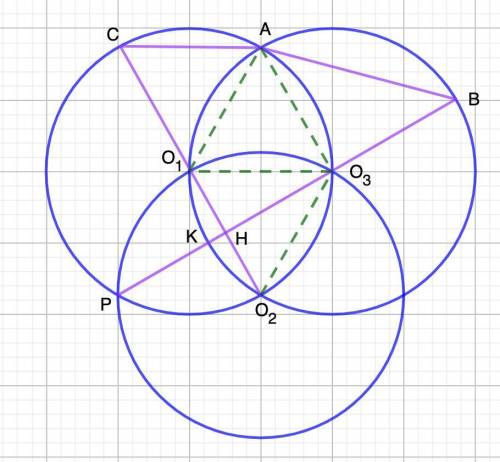
Соединим точки О₁ и А; А и О₃; О₁ и О₃; О₂ и О₃.
Так как три окружности проходят через центры друг друга ⇒их радиусы равны. Пусть радиусы всех окружностей равны R.
1. Рассмотрим Окр. О₁R и Окр. О₂R.
СО₂⊥РО₃ (свойство пересекающихся окружностей)
⇒∠СНВ=90°.
2. Рассмотрим ΔО₁АО₃
О₁А=АО₃=О₃О₁=R
⇒ΔО₁АО₃ - равносторонний.
⇒∠АО₁О₃=60°=∪ АО₃ (центральный)
3. Рассмотрим ΔО₂О₁О₃=равносторонний.
О₁О₃=О₃О₂=О₁О₂=R
⇒∠О₂О₁О₃=60°=∪ О₃О₂ (центральный)
4. ∪ АО₃О₂=∪ АО₃+∪ О₃О₂=60°+60°=120°
5. Рассмотрим Окр. О₁R.
∠О₂СА=120°:2=60° (вписанный)
6. Рассмотрим ΔО₁О₃О₂ равносторонний.
О₃Н⊥РО₃ (п.1)⇒О₃Н-высота, биссектриса (свойство равнобедренного Δ)
⇒∠НО₃О₁=30°=∪ О₁К (центральный)
7. ∠О₁О₃А=60° (ΔО₁АО₃-раввносторонний)
⇒∪ АО₁=∠О₁О₃А=60° (центральный)
8. ∪ КО₁А=∠О₁О₃А+∠КО₃О₁=60°+30°=90°
∠КВА=90°:2=45°(вписанный)
9. Сумма углов четырехугольника равна 360°.
⇒∠САВ=360°-(90°+60°+45°)=165°
![\sqrt[n]{x}](/tpl/images/0258/0436/b773b.png)
Плоскость Омега, параллельная прямой С, пересекает плоскости Альфа и Бета по прямым а и b соответственно, значит прямые а и b лежат в плоскости Омега,
Плоскости Альфа и Бета пересекаются по прямой С, Плоскость Омега, пересекает плоскость Альфа по прямой а, значит
прямые а и С лежат в одной плоскости Альфа,
Плоскости Альфа и Бета пересекаются по прямой С, Плоскость Омега, пересекает плоскость Бета по прямой b, значит
прямые b и С лежат в одной плоскости Бета
Плоскость Омега, параллельная прямой С,значит пряммая С паралельна какойто прямой d, лежащей в плоскости
Две плоскости, содержащие параллельные прямые, пересекаются по прямой, параллельной данным.
Плоскость Бета содержит прямую С, которая паралельна прямой d, лежащей в плоскости Омега, значит пряммая по которой пересекаются плоскости Бета и Омега (пряммая а) паралельна прямой С
Плоскость Альфа содержит прямую С, которая паралельна прямой d, лежащей в плоскости Омега, значит пряммая по которой пересекаются плоскости Альфа и Омега (пряммая b) паралельна прямой С
если пряммая, что не лежит в плоскости, паралельна прямой лежащей в этой плоскости, то пряммая паралельна плоскости
(пряммая а) (не лежащая в плоскости Бета) паралельна прямой С, лежащей в плоскости Бета, значит пряммая а паралельна плоскости Бета
(пряммая b) (не лежащая в плоскости Альфа) паралельна прямой С, лежащей в плоскости Альфа, значит пряммая b паралельна плоскости Альфа.
Доказано