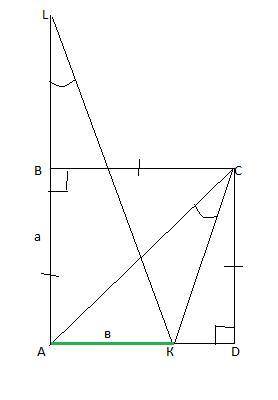
Сторона квадрата ABCD равна a. На стороне AD лежит точка K, а на продолжении стороны AB за точкой B лежит точка L. Чему равна длина отрезка AL, если ∠ACK=∠ALK, и AK=b?
Объяснение:
Пусть ∠АLК=α
1) ΔАКL -прямоугольный, tg∠АLК=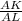
, AL=в / tgα.
2)ΔACD -прямоугольный, АС=а√2, по т. Пифагора.
ΔКCD -прямоугольный, по т. Пифагора, КС=√(а²+(а-в)²).
3)ΔACК, угол ∠АСК=α.
По т. косинусов выразим cosα :
АК²=АС²+КС²-2АС*КС*cosα,
в²=2а²+а²+(а-в)²-2*а√2*√(а²+(а-в)²)*cosα,
2*а√2*√(а²+(а-в)²)*cosα =-в²+2а²+а²+(а-в)² ,
2*а√2*√(а²+(а-в)²)*cosα =-в²+4а²-2ав+в² ,
2*а√2*√(а²+(а-в)²)*cosα =2а(2а-в) ,
cosα =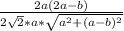 
cosα =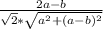 
, tg²α=1:( cos²α)-1 , tgα =
,
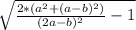tgα =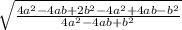
=
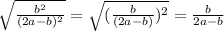
4)AL=в/tgα , AL=в: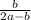 
, AL=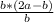
, AL=2a-b .
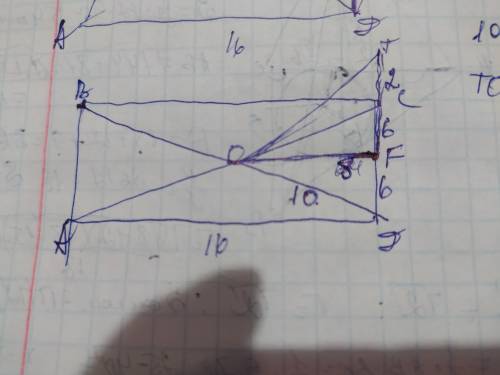
ответ: ОТ=2√17см
Объяснение: обозначим вершины прямоугольника ABCD с диагоналями АС и ВД, а точку их пересечения О. Одна диагональ прямоугольника делит его на 2 равных прямоугольных треугольника в которых стороны являются катетами а диагональ гипотенузой. Найдём диагональ прямоугольника по теореме Пифагора:
АС²=ВД²=АВ²+ВС²=12²+16²=256+144=400;
АС=ВД=√400=20см
Диагонали прямоугольника равны и пересекаясь делятся пополам поэтому АО=СО=ВО=ДО=20÷2=10см
СF=ДF=12÷2=6см
ОF является проекцией ТО на площадь прямоугольника. Рассмотрим полученный ∆ДОF. Он прямоугольный, ОF и ОД- катеты, а ОД- гипотенуза. Найдём OF по теореме Пифагора:
ОF²=ОД²-FД²=10²-6²=100-36=64;
ОF=√64=8см. Рассмотрим ∆OTF. Он также прямоугольный и ОF и ТF- катеты, а ОТ - гипотенуза. Найдём ОТ по теореме Пифагора: ОТ²=OF²+TF²=8²+2²=64+4=68;
OT=√68=2√17см
Пусть x- мера углов
Тогда угол ABO=2x, угол BAO=7x
рассмотрим тр. ABO.
180=90+2x+7x
9x=90
x=10
Значит угол ABO=20, угол BAO=70
угол BAO = BCO = 70 - свойство углов ромба.
Тогда угол ABC=180-70-70=40
угол OBC=40-20=20
Значит:
угол A=C=140
угол B=D=40
угол BAC=BCA=CAD=ACD=70
угол ABO=CBO=ADO=CDO=20