1), 2), 6), 8).
Объяснение:
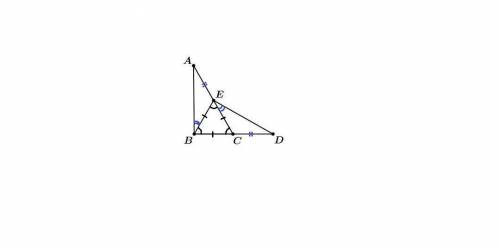
ΔАВС = ΔDEB,
АВ = DE, АС = DB, значит ВС = ВЕ, т.е. ΔВЕС равнобедренный
В равных треугольниках против равных сторон лежат равные углы, значит
∠DBE = ∠ACB, тогда
ΔВЕС равнобедренный с основанием ВС.
Итак, ВЕ = ЕС = ВС, т.е. ΔВЕС равносторонний.
∠АВЕ = ∠АВС - ∠ЕВС
∠DEC = ∠DEB - ∠BEC
∠АВС = ∠DEB из равенства треугольников,
∠EBC = ∠BEC, как углы равностороннего треугольника, значит
∠АВЕ = ∠DEC.
АЕ = АС - ЕС
CD = DB - BC
AC = DB по условию,
ЕС = ВС, так как ΔВЕС равносторонний, значит
АЕ = CD.
1) Треугольник BCE равнобедренный - верно.
2) Треугольник BCE равносторонний - верно.
3) ∠ABC = 90° - нельзя утверждать.
4) Треугольник ECD равнобедренный - нельзя утверждать.
5) AE = BC - нельзя утверждать.
6) AE = CD - верно.
7) ∠ABE = ∠CDE - нельзя утверждать.
8) ∠ABE = ∠CED - верно.
Пусть АЕ = х см , тогда
1) Рассмотрим ∆ АВЕ ( угол АЕВ = 90° ) :
Сумма острых углов в прямоугольном треугольнике равна 90° =>
угол ВАЕ + угол АВЕ = 90°
угол АВЕ = 90° - 60° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы =>
АВ = 2 × АЕ = 2х
АВ = CD = 2x
Пусть МО = у , тогда ОN = 16 + y
2) Рассмотрим ∆ АВС :
АМ = МВ , МО || ВС => АО = ОС
MO - средняя линия
ВС = 2 × МО = 2у
ВС = EK = 2y
3) Рассмотрим ∆ САD :
CN = ND , ON || АD => CO = OA
ON - cредняя линия
AD = 2 × ON = 2 × ( 16 + y )
Но с другой стороны ,
АD = AE + EK + KD = x + 2y + x = 2x + 2y
2 × ( 16 + y ) = 2x + 2y
32 + 2y = 2x + 2y
2x = 32
x = 16 cm => AE = KD = 16 cm
AB = CD = 2x = 2 × AE = 2 × 16 = 32 cm
P abcd = AB + BC + CD + AD = 32 + 2y + 32 + 2y + 32 = 4y + 96
4y + 96 = 144
4y = 48
y = 12 cm => BC = EK = 12 cm
Значит, ВС = 24 см , АD = 56 cm
ОТВЕТ: 24 см ; 56 см