1. В прямоугольнике диагонали образуют треугольники, у которых углы при основании равны.
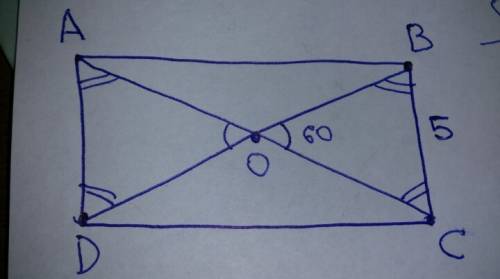
2. Угол BOC=AOD (как вертикальные); рассмотрим треугольник BOC: угол OBC=OCB, ВС=5 см. Т.к. в треугольнике сумма углов равна 180 градусам, то 180-60=120 гр, а 120:2=60 гр. Значит, OBC=OCB=60 гр., а треугольник BOC - равносторонний.
3. Треугольники BOC и AOD равны, т.к. угол BOC=AOD (как вертикальные), DAO=OCB=ADO=OBC (как внутренне накрест лежащие). BC=AD=BO=OC=AO=DO=5 см.
Значит, диагональ AC=DB (т.к. точка О середина пересечения диагоналей) = 10 см
ответ: AC=DB=10 cv
углы при основании (угол 2) и (угол 3) равны друг другу
угол 1 + угол 2 + угол 3 = 180 градусов (по теореме о сумме углов треугольника)
угол 2 = угол 3 = (180 - угол 1)/2=(180-30)/2=150/2=75 градусов
ответ: каждый угол при основании равен 75 градусам.