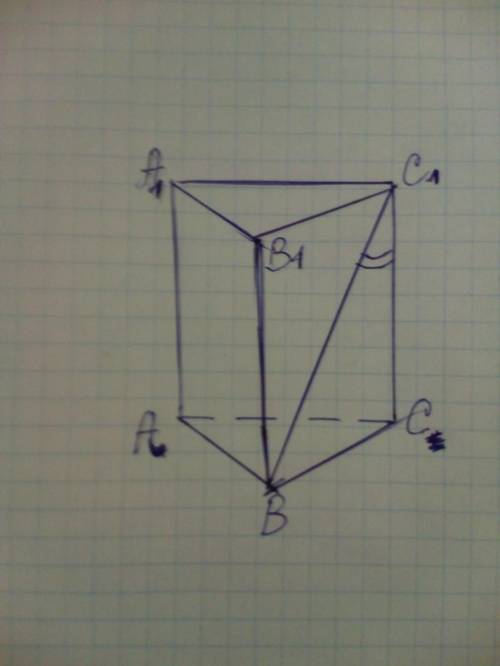
Диагональ ВС₁=а, образует с боковым ребром СС₁ угол β, ∠ВС₁С=β, Из ΔС₁СВ (∠С=90°); ВС=С₁В*sinβ=a*sinβ; CC₁=С₁В*cosβ=a*cosβ
Площадь боковой поверхности призмы равна 3*ВС*СС₁=3a*sinβ*a*cosβ=1.5a²sin2β
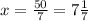 см
см
Відповідь: 3а²(sin2В)/2.
Пояснення:
Бічна грань - прямокутник.
ЇЇ розміри -аsin В*аcos В = а²(sin2В)/2.
Площа бічної поверхні призми складає з 3 граней, тоді Sбок = (а²(sin2В)/2)*3 =