Площадь полной поверхности призмы равна сумме площадей двух её оснований и площади боковой поверхности.
Боковые грани прямой призмы - прямоугольники. Площадь боковой поверхности равна периметру основания, умноженному на высоту призмы.
S=P•h=(10+12+20)•3=126 (ед. площади)
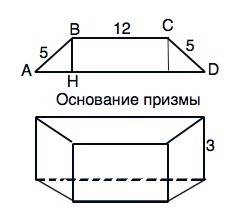
Площадь основания - площадь трапеции АВСD.
Высота равнобедренной трапеции, проведенная из тупого угла, делит большее основание на отрезки, меньший из которых равен полуразности, больший - полусумме оснований.
АН=(АD-BC):2=8:2=4
НВ=(AD+DC):2=32:2=16
Из ∆ АВН по т.Пифагора ( или обратив внимание на то, что ∆ АВН - египетский) находим ВН=3
S осн=3•16=48 Оснований у призмы 2.
S полн=126+2•48=222 (ед. площади)
хм=(-1+1)/2=0
ум=(6-2)/2=2.
Находим расстояние АМ по формуле расстояния между двумя точками. Это будет радиус окружности:
АМ=корень (((-1-0)^2+(6-2)^2)=корень (91+16)=корень из 17.
Уравнение окружности
(х-х0)^2+(y-y0)^2=R^2.
х^2+(y-2)^2=17.
Уравнение прямой, проходящей через точку М (0.2) параллельно оси Ох: у=2.
А прямая, проходящая вертикально через центр, это будет сама ось Оу: х=0.