Дана равнобедренная трапеция abcd. пенпендикуляр, проведенный из вершины b к большому основанию ad, делит это основание на два отрезка, больший из которых равен 7 см. найдите среднюю линию трапеции

👇

Ответ:

Мирандалина1414

02.03.2023

Средняя линия трапеции равна половине суммы длин оснований. Точку пересечения высоты, опущенной из вершины В с основанием обозначим через М, тогда АМ=х, а МD=7. Из вершины С также проведем высоту к AD точка пересечения N.Так трапеция равнобокая, то AM=AN=x. А длина ВС=7-х, вся длина AD=7+x. Тогда средняя линия трапеции равна (BC+AD)/2, т.е.(7-х+7+х)/2=14/2=7

4,4(42 оценок)

Открыть все ответы

Ответ:

jekaroikp00z44

02.03.2023

Рисуем треуг АВС(только не равнобедренный). Где АС основание, а В вершина. Из вершины В к основанию АС проводим высоту-ВН (ВН перпендикулярен АС). Так же из вершины В проводим биссиктрису- BD ( делит угол ABC пополам т.е. ABC/2=<АВД=<ДВС). У меня получилось что Д стоит правее А, а Н стоит левее С прощения буквы обозначении буду писать русскими т.к.не корректно сохраняется, этот ответ уже пишу второй раз.(в первый раз ответ не полностбю сохранился) Дано: треуг АВС, <ВАС=40°,<ВСА=60°, ВД-биссектр., ВН-высота. Найти:<ДВН=? Решение: Рассмотрим треуг АВС 1) <ВАС=40° по усл.задачи 2) <ВСА=60° по усл.задачи 3) <АВС=180°- ( <ВАС+ <ВСА)=180°-(40°-60°)=80° (т.к. сумма всех угл.треуг. равна 180°) 4) ВД-биссектр. по усл.задачи и значит <АВД=<ДВС=80°/2=40° Рассмотрим треуг НВС 1)<ВСН=60° по усл.задачи 2)<ВНС=90° т.к. ВН является высотой по усл.задачи 3)<НВС=180°- ( <ВНС +<ВСН)= 180°-(90°+60°)= 30° <ДВН=<ДВС -<НВС= 40°-30°=10° ответ:<ДВН=10° ЗАДАЧА НОМЕР 2. Рисуем треуг. равноб.треуг АВС, где АС-основание, а из вешины В проведена к основанию ВМ медиана(делящая АС пополам АМ=МС) Дано: треуг АВС, АВ=ВС=53см, АС=56см, ВМ-медиана Найти: ВМ=? Решение: Рассмотрим треуг АВС 1) треуг АВС-равнобед. по св-ву равноб.треуг.(если в треуг. 2стор.=то треуг.равноб) т.к. АВ=ВС=53см по усл. Задачи 2) АС=56см по усл.задачи 3) ВМ-медиана по усл.задачи, а значит АМ=МС=56/2=28см. 4) <ВМС=90° т.к. ВМ также является и высотой по свойсвам равнобед треуг(в равноб.треуг.медиана проведён.к основ, является высотой и биссектрисой) Рассмотрим треуг.МВС 1) треуг. МВС прямоуг.треуг. т.к. <ВМС=90° 2) ВС=53см по усл.задачи 3) МС=28см 4) По теореме Пифагора найдём ВМ=? а^2+в^2=с^2 ВМ^2=ВС^2-МС^2 ВМ^2=53^2-28^2=2809-784=2025 ВМ=√2025=45см ответ: ВМ=45см.

4,7(51 оценок)

Ответ:

NastenkaDrow

02.03.2023

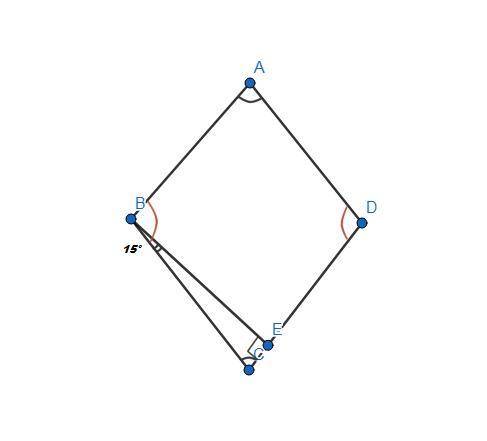
Дано:

ABCD - ромб.

ВЕ - высота.

∠АВС - тупой.

∠ЕВС = 15°.

Найти:

∠АВС = ? (или ∠АDС, это не столь важно, так как они равны.)

1. Рассмотрим треугольник ЕВС - прямоугольный. ∠ВСE (∠BCD) = 90°-∠ЕВС = 90°-15° = 75° (по свойству прямоугольного треугольника - сумма острых углов прямоугольного треугольника равна 90°). 2. Ромб - это тоже параллелограмм, а засчёт того, что противоположные стороны параллельны (ВС║AD; АВ║CD - по определению параллелограмма), то сумма односторонних углов при параллельных прямых ∠ABC+∠BCD = 180°. ⇒ ∠ABC = 180°-∠BCD = 180°-75° = 105°.3. Противоположные углы параллелограмма равны (на рисунке они выделены дугами). Следовательно, каждая пара углов равна по 75° и 105°. Больший угол ромба равен 105°.

ответ: 105°.