ответ: a) 62°; б) 118°
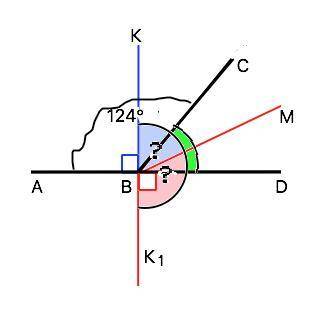
Объяснение: Вопрос явно неполный - не указан второй угол. Правильно: Углы ABC и BCD – смежные, причем угол ABC равен 124 градуса. Найдите угол между перпендикуляром, проведенным из точки B к прямой AD и биссектрисой угла CBD.
* * *
Сумма смежных углов 180°, поэтому ∠СВD=180°- ∠ABC=180°-124°=56°.
Обозначим биссектрису угла СВD как ВМ. Биссектриса угла делит его пополам, поэтому ∠СВМ=∠DBM=56°:2=28°
У задачи 2 варианта решения.
а) Перпендикуляр ВК к прямой AD лежит в той же полуплоскости, что луч ВС. Тогда искомый угол КВМ=∠КВD-∠MBD=90°-28°=62°
б) Перпендикуляр ВК1 лежит во второй полуплоскости. Тогда искомый угол К1ВМ=∠K1BD+∠DBM=90°+28°=118°
Шар можно описать около призмы, если она прямая и ее основания являются многоугольниками, вписанными в окружность. Центр шара лежит на середине высоты призмы, соединяющий центры окружностей, описанных около основания призмы.
Полуплоскость ограничена прямой, параллельной боковому ребру призмы и проходящей через центр шара.
Поскольку призма правильная, то в основе лежит квадрат, тогда диагональ АС: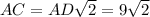 см
см
По теореме Пифагора из прямоугольного треугольника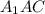 , найдем высоту призмы.
, найдем высоту призмы.
Под корнем отрицательное число, что-то в условии не так