Отрезки ае и dc пересекаються в точке в, являющейся серединой каждого из них. докажите, что треугольники abc и ebd равны.

👇

Ответ:

mk515

16.12.2021

ΔАВС = ΔЕВД по 1-му признаку равенства треугольников: Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Действительно,
АВ = ВЕ, т.к. точка В - середина отрезка АЕ;
ДВ = ВС, т.к. точка В - середина отрезка ДС
угол ДВЕ = углу АВС как вертикальные.

4,4(53 оценок)

Открыть все ответы

Ответ:

gyulmalievasab

16.12.2021

Проведем DK⊥SC.
ΔDKC = ΔBKC по двум сторонам и углу между ними (DC = BC как стороны квадрата, КС - общая, углы при вершине С равны, так как боковые грани - равные равнобедренные треугольники).
Тогда и ВК⊥SC, значит
∠DKB - линейный угол двугранного угла при боковом ребре пирамиды.
Обозначим его α.
sinα = 12/13

SC⊥DKB (ребро SC перпендикулярно двум пересекающимся прямым этой плоскости), ⇒
SC⊥OK.
Тогда отрезок ОК параллелен высоте треугольника ASC, проведенной из вершины А (обозначим ее h), и равен ее половине.
Sasc = 1/2 · SC · h = 1/2 · SC · 2OK = SC·OK = 7√13 ( 1 )

ΔOKD: OK = KD · cos (α/2)

Угол α тупой, т.к. sin(α/2) = OD/DK > OD/DC = 1/√2
cos α = - √(1 - sin²α) = - √(1 - 144/169) = - √(25/169) = - 5/13

cos (α/2) = √((1 + cos α)/2) = √((1 - 5/13)/2) = √(8/26) = √(4/13) = 2/√13

Вернемся к ΔOKD:
ОК = KD · cos (α/2) = KD · 2/√13
Подставим в равенство (1):
SC · KD · 2/√13 = 7√13
SC · KD = 7√13 · √13 / 2 = 91/2
Но KD - высота боковой грани SCD, проведенная к ребру SC.
Sscd = 1/2 · SC · KD = 1/2 · 91/2 = 91/4
Тогда площадь боковой поверхности:
Sбок = 4 · Sscd = 4 · 91/4 = 91

4,6(83 оценок)

Ответ:

мария2386

16.12.2021

Задача №1.

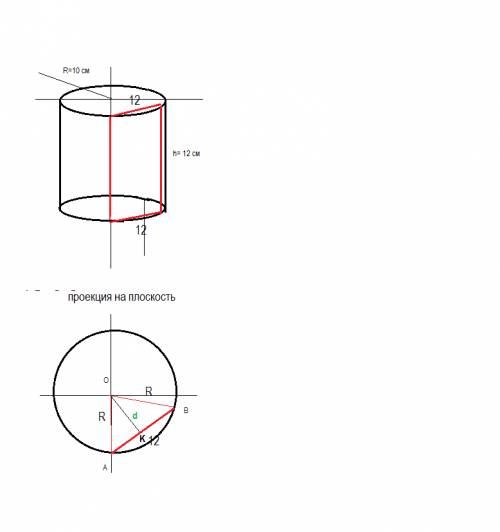
на проекции видно, что треугольник АОВ - равнобедренный ОА = ОВ =R =10 см

основание треугольника АВ= 12 см (это сторона квадратного сечения - она равна высоте h= 12 см)

расстояние от оси цилиндра до секущей плоскости - высота d

высота d делит сторону АВ на равные части , тогда АК=АВ/2=12/2= 6 см

тогда по теореме Пифагора

d^2 = OA^2 - AK^2= R^2 - AK^2 = 10^2 - 6^2 = 64= 8^2

d= 8 см

ответ 8 см расстояние от оси цилиндра до секущей плоскости.

Задача №2

Из правил сервиса: "Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач".