так как средняя линия равна полусумме оснований то надо найти второе (большее основание), для этого проведем высоту из тупого угла к большему основанию. она отсечет от трапеции прямоугольник, то есть одна из частей разделенного высотой большего основания равна 10. найдем второй кусок большего основания дл я этого рассмотрим прямоугольный треугольник который образовала большая боковая сторона и высота. т.к один из острых углов в прямоугольном треугольнике равен 60 градусам, то 2ой угол равен 90-60=30 градусов. так каак в прямоугольном треугольнике катет лежащий против угла в 30 градусов (а это и есть нужный нам второй кусок большего основания) равен половине гипотенузы, то он равен 8/2=4. тогда большее основание равно сумме двух кусков то есть 10+4=14. средняя линия равна полусумме оснований, то есть (10+14)/2=24/2=12.
ответ:12.
p.s понимаю что на словах ничего не понятно поэтому вложен рисунок.

См. рисунок во вложении
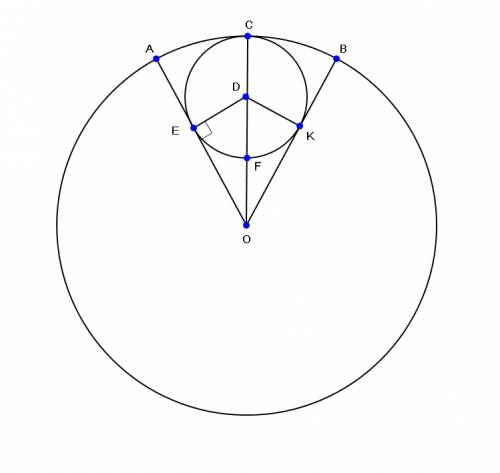
АОВ- центральный угол сегмента
Площадь сегмента S=пи*R^2*(угол AOB)/360, где R -радиус основной окружности.
Обозначим r - радиус вписанной окружности
DE - перпендикуляр из центра вписанной окружности на радиус AO.
CD=DF=DE=r
R=3*r
CO=R, CD+DF=2*r, значит, FO=r
DF+FO = 2*r
В треугольнике OED sin угла(EOD)=DE/DO=1/2
Угол EOD=30 градусов, он равен половине центрального угла сегмента (это очевидно из рассмотрения треугольников EDO и DOK), значит, центральный угол равен 60 градусов
S=пи*R^2*60/360=24*пи, откуда R^2=144, R=12
r=R/3=4
Длина вписанной окружности hfdyf 2*пи*r=8*пи
9х=90°; х=10°, значит угол АВО=10°, а угол ВСА=80°.