ответ:Задание 2
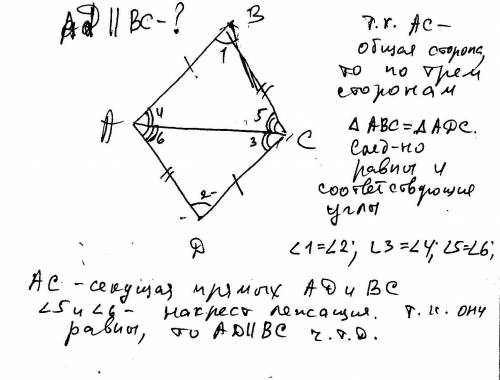
Пересекаются две прямые с и а,и возникают вертикальные углы,причём-противоположные углы равны между собой,т е
2=4. 1=3
Если угол 4 равен 65 градусов,то и угол 2 тоже равен 65 градусов
Общая сумма четырёх вертикальных углов Равна 360 градусов,углы 1 и 3 можем узнать следующим образом
[360-(65+65)]:2=230:2=115
Угол 1 равен 115 градусов и угол 3 тоже равен 115 градусов
Можно было и иначе решить
Угол 1 и угол 4 являются смежными углами,их сумма равна 180 градусов
180-65=115 градусов
Пересекаются два отрезка c и b и возникают 4 вертикальных угла
5=7. 4=6
Если угол 7 равен 120 градусов,то 120 градусов равен и угол 5
Углы 4 и 6 равны
[360-(120+120)]:2=120:2=60 градусов
Можно решить иначе
Углы 4 и 7 смежные,их сумма равна 180 градусов,угол 4 равен
180-120=60 градусов
Задание 1
Если две параллельные прямые пересечены секущей,то накрест лежащие углы равны
Угол 1 равен углу 2
Узнаём чему равен угол 2,он является смежным для угла 121 градус
Сумма смежных углов равна 180 градусов
180-121=59 градусов
Значит и угол 1 равен тоже 59 градусов
Объяснение:
Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
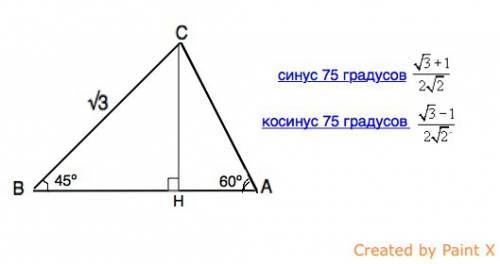
Из суммы углов треугольника найдем угол С:
∠С=180º-45º-60º=75º
В прямоугольном ⊿ ВНС угол ВСН=90º-45º=45º
⊿ ВНС - равнобедренный, СН=ВН=ВС•sin 45º=(√3•√2):2
В ⊿ АНС сторона АС=СH:sin 60º
AC=[(√3•√2):2]:(√2):2=√2
АВ=ВН+АН
АН противолежит углу НСА, равному 90º-60º=30º
АН=АС:2=(√2):2
АВ=(√3•√2):2+(√2):2=(√3+1):√2
––––––––––––
Или по т. синусов:
АВ:sin75=BC:sin60
sin 60º=(√3):2
sin 75º=(√3+1):2√2 ( из таблицы тригонометрических функций)
АВ:(√3+1):2√2=(√3):[(√3):2]⇒
AB=(√3+1):√2
--------------
или по т.косинусов
AB²=BC²+AC²- 2BC•AC•cos75º
cos 75º=(√3-1):2√2
AB²=3+2- 2√6•((√3-1):2√2)⇒
AB=√(2+√3)
Оба найденных значения АВ равны - проверьте, возведя их в квадрат.
[√(2+√3)]²=[(√3+1):√2]²