Смотри рисунок на прикреплённом фото.
1) ΔАСD ~ ΔABС по 1-му признаку подобия прямоугольных треугольников: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны. А у ΔАСD и ΔABС общий острый угол А.
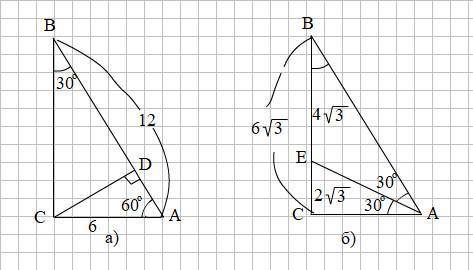
2) Катет АС прямоугольного ΔАВС лежит против угла ∠В = 30°, значит АС равен половине гипотенузы АВ: АС = 0,5АВ = 0,5·12 = 6 (см).
Найдём коэффициент подобия ΔАСD и ΔABС по отношению их гипотенуз АС : АВ = 6/12 = 1/2. Следовательно, коэффициент подобия этих треугольников k = 1/2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S(ΔACD) : S(ΔABC) = k² = 1 : 4.
3) Найдём величину катета ВС, используя теорему Пифагора:
ВС = √(АВ² - АС²) = √(12² - 6²) = √108 = 6√3 (см)
Известно, что биссектриса угла делит противолежащую сторону на отрезки, пропорциональные прилежащим к углу сторонам. Поэтому СЕ : ВЕ = АС : АВ = 1/2.
Тогда СЕ = 1/3 · ВС = 2√3 (см) и ВЕ = 2/3 · ВС = 4√3 (см)
Пингвины ведут совершенно необычный образ жизни. С чем это связано? Может с тем, что пингвин относится к одним из немногих нелетающих птиц… А может, из-за того, что он использует свои крылья как плавники…А может потому, что самка и самец по очереди выращивают и выкармливают свое потомство…
Когда проходит период ухаживания пингвинов, они заводят потомство. Когда самка являет свету яйцо, его ни в коем случае нельзя опускать на снег, иначе в результате переохлаждения искра жизни в яйце потухнет. Так начинается жизнь пингвинов…
Самка передает очень аккуратно яйцо на лапы самца, который благодарит ее в ритуале поклонов, потрясений хвостом. Получив яйцо, он осторожно окутывает его своей брюшной складкой на лапах, где и греет его на протяжении двух месяцев, пока самка находится в поиске пищи для себя и своей семьи. Тем временем самец с яйцом пристраивается к самым теплым членам своего собратства. Этот ритуал тоже очень редок, почему пингвины занесены в Красную книгу
ВН = СК = 7,5 · 2 = 15 см
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
АН = √(АВ² - ВН²) = √(17² - 15²) = √(289 - 225) = √64 = 8 см
ΔАВН = ΔDCK по катету и гипотенузе (АВ = CD по условию, ВН = СК как высоты трапеции), ⇒
DK = AH = 8 см
Если в четырехугольник вписана окружность, то суммы противоположных сторон равны:
AD + BC = AB + CD = 17 + 17 = 34 см
AD = AH + HK + KD = 8 + HK + 8 = HK + 16
Так как НК = ВС:
AD + BC = 34
AD = BC + 16
2BC + 16 = 34
BC = (34 - 16)/2 = 18/2 = 9 см
AD = 9 + 16 = 25 см