60 см
Объяснение:
Дана прямоугольная трапеция, BC - малое основание,AD- большое основание, <A=<B = 90, <D = 30
Радиус вписанной окр-ти по т.Пифагора
r = √(13^2 - 12^2) = 5
Проведем из точки C к AD высоту CH = AB = 2r = 10
Тр-к CDH - прямоугольный
CD = CH/sin30 = 10/0,5 = 20
HD = CHcos30 = 5√3
BC = AH = x
AD = AH + HD = x + 5√3
p = P/2 = (BC + AB + CD + AD)/2 = (x + 10 + 20 + x + 5√3)/2 = x + 15 + 2,5√3
S = p*r = (x + 15 + 2,5√3)*5
S = (BC + AD)/2 * AB = (x + x + 5√3)/2 * 10 = (2x + 5√3)*5
Приравняем
(x + 15 + 2,5√3)*5 = (2x + 5√3)*5 |:5
x + 15 + 2,5√3 = 2x + 5√3
х = 15 - 2,5√3
P = 2p = 2*(x + 15 + 2,5√3) = 2* (15 - 2,5√3 + 15 + 2,5√3) = 60 см
ответ: а=4 .
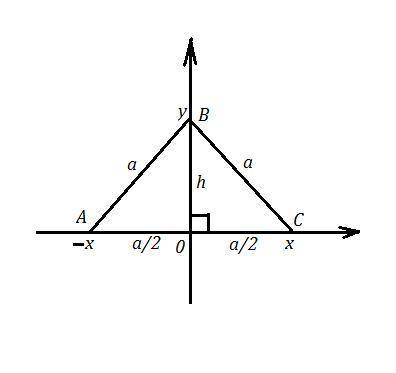
ΔАВС - правильный ⇒ все его стороны равны "а" . Высота равностороннего треугольника является и медианой. Так как ОХ⊥ОУ , то если две вершины лежат на оси ОХ, тогда третья вершина лежит на оси ОУ. Пусть вершины А и С лежат на оси ОХ, тогда координаты точки А(х,0) , а координаты точки С(-х,0). Вершина В лежит на оси ОУ и её координаты будут В(0,у) .
По условию сумма всех координат равна:
(-х+0)+(х+0)+(0+у)=2√3 ⇒
у=2√3 (2√3>0 ⇒ точка В лежит в верхней полуплоскости) ⇒ высота ВО=h=2√3 .
По теореме Пифагора из прямоугольного ΔАВО имеем: 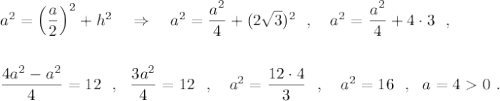
Длина сторона правильного треугольника равна 4 .
Т.к. пирамида правильная, основание высоты МО совпадает с центром вписанной в основание окружности.
МО⊥АВСД.
МО=3а, АД=а, АО=ОС.
Искомые углы - это углы МНО и МАО.
ОН=АД:2=а/2
tg∠МНО=МО:ОН=3а: 0,5а=6
По таблице тангенсов это тангенс угла 80°30’
tg∠МАО=МО:ОА
ОА=АС:2
АС=а√2 ( как диагональ квадрата)
ОА=(а√2):2
tg∠МАО=3а:[(а√2):2] ≈ 4,243
По таблице тангенсов это тангенс угла 76°42'