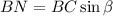
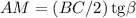
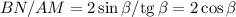
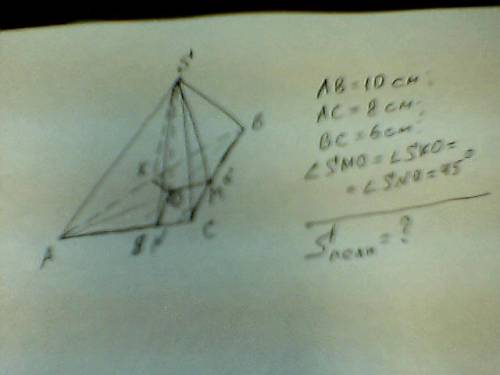
Рисунок к задаче - во вложении.
SK, SM, SN - высоты (апофемы) боковых граней. SO - высота пирамиды.
Прям. тр-ки SOK, SOM, SON - равны, т.к. SO - общий катет и углы равны по условию.
Значит т. О - центр вписанной окр-ти для тр-ка АВС.
Тр-к АВС - прямоугольный, т.к. для него справедлива теорема Пифагора:
10² = 8² + 6²
Тогда его площадь:
S(ABC) = 6*8/2 = 24 cm²
С другой стороны:
S(ABC) = p*r, где р - полупериметр, а r - радиус вписанной окр-ти.
р = (10+8+6)/2 = 12 см. r = 24/12 = 2 cm.
Теперь, например, из тр-ка SOM находим апофему:
SM = r/cos45 = r*√2 = 2√2 см.
Теперь находим полную пов-ть пирамиды, сложив площади четырех тр-ов:
Sполн = S(ABC) + S(SAB) + S(SAC) + S(SBC) = 24 + (10*2√2 + 8*2√2 + 6*2√2)/2 =
= 24(1+√2) cm²
ответ: 24(1+√2) см².
В плоскости CDK проведем прямую II CD, отложим на ней отрезок равный CD, и обозначим конец K1
KDCK1 - прямоугольник.
K1C перпендикулярно СD. Поскольку CD перпендикулярно МС, то KK1 перпендикулярно МК1 (эта прямая лежит в плоскости МСК1) Поэтому треугольник МК1К прямоугольный. И треугольник МСК1 тоже - К1СМ - плоский угол двугранного ула между 2 перпендикулярными плоскостями.
Отсюда
МК1^2 = CM^2+CK1^2;
KK1^2 = MK^2 - MK1^2; Собираем все это, получаем
СD^2 = 17^2 - 8^2 - 9^2 = 144 = 12^2;
CD = 12