
∠A = ∠C = 55° и ∠B = ∠D = 125°.
Объяснение:
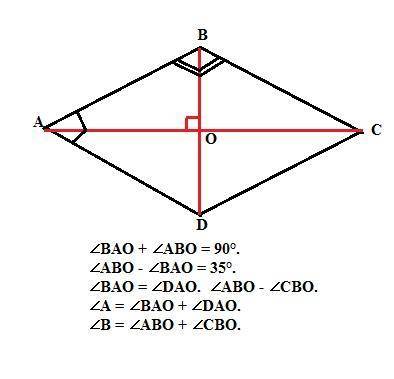
Диагонали ромба взаимно перпендикулярны. Следовательно, они со стороной ромба образуют прямоугольный треугольник. Сумма острых углов прямоугольного треугольника равна 90°, а их разность равна 35° (дано).
Пусть один из углов равен х градусов. Тогда второй равен х+35 градусов.
Значит 2х = 90-35 = 55°. И один из углов треугольника равен 55:2 = 27,5°.
Тогда второй угол равен 27,5+35 = 62,5°.
В ромба диагонали являются биссектрисами его углов. Следовательно, углы ромба равны удвоенным градусным мерам найденных углов прямоугольного треугольника.
Противоположные углы ромба равны.
Углы ромба равны 125° и 55°.
Проверка: углы ромба, прилежащие к одной стороне, в сумме равны 180°.
125+55 = 180°.
ответ: 5*
решение: мы знаем все углы, это очень хорошо
рассмотрим треугольник образованный после того как мы посторили высоту, он прямоугольный, тк высота это один из катетов жэтого треугольника. Ещё мы знаем угол острого угла данного нам изначально прямоугольного треугольника - это 50*. 180-50-90=40* это один из 3х образовавшихся углов в прямом углу нашего карневого треугольника.
2й угол из тех трех это 45*, так как нам дана биссектриса, которая делит наш прямой угол на два ровных угла по 45*
на и найдем оставшийся 3й угол, весь угол(90*)-45*-40*=5*