Задача очень простая, но прикольно сформулирована, поэтому я берусь за решение :))
Если провести окружность радиусом 5 с тем же центром, что и заданная окружность, то она пересечет хорду АВ в 2 местах - в точке С, удаленной от А на 2, и в точек С1, удаленной от В тоже на 2 :)) То есть АС1 = 28. Если из точки А провести прямую через центр до пеересечения с внутренней окружностью, то её отрезки будут от А до малой окружности R - 5, от А до второй точки пересечения с малой окружностью R + 5; R - радиус окружности, который надо найти.
(R - 5)*(R + 5) = 2*28;
R^2 = 56 + 25 = 81;
R = 9;
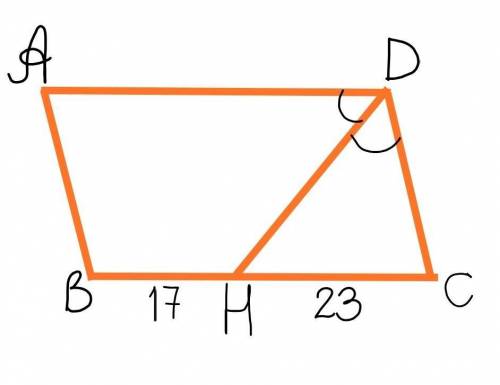
Так как противоположные стороны параллелограмма параллельны, то угол СНD=угол ADH как накрест-лежащие при параллельных прямых AD u BC и секущей DH.
Биссектриса делит угол на два равных угла.
Следовательно угол СDH=угол ADH.
Исходя из найденного: Угол СHD=угол CDH.
Тогда ∆CHD – равнобедренный с основанием HD.
У равнобедренного треугольника боковые стороны равны, тоесть CD=CH=23 см
Противоположные стороны параллелограмма попарно равны.
Следовательно: AD=BC=BH+HC=17+23=40 см; AB=CD=23 см.
Периметр параллелограмма – это сумма длин всех его сторон.
Тоесть Р=AD+AB+BC+CD=40+23+40+23=126 см.
ответ: 126 см.