Объяснение:
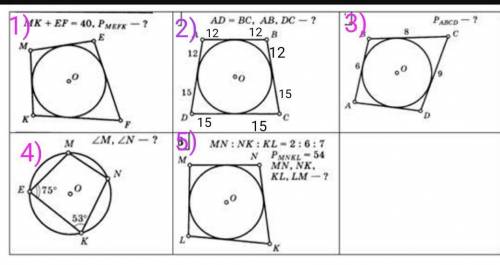
1)
В четырехугольник можно вписать окружность, если сумма противоположных сторон равна сумме двух других противоположных сторон.
МК+ЕF=ME+KF.
P=2(MK+EF)=2*40=80ед.
ответ: 80ед.
2)
АD=BC.
Две касательные проведенные из одной точки равны между собой.
АВ=2*12=24ед
DC=2*15=30ед.
ответ: АВ=24ед; DC=30ед.
3)
В четырехугольник можно вписать окружность, если сумма противоположных сторон равна сумме двух других противоположных сторон.
АВ+СD=BC+AD.
P=2(AB+CD)=2(6+9)=2*15=30ед.
ответ: 30ед.
4)
Четырехугольник можно вписать в окружность, если сумма противоположных углов равна 180°
<М+<К=180°. →
<К=180°-<К=180°-53°=127°
Аналогично для двух других углов
<Е+<N=180°
<N=180°-<E=180°-75°=105°
ответ: <К=127°; <N=105°
5)
В четырехугольник можно вписать окружность если сумма противоположных сторон равна сумме двух других противоположных сторон
MN+KL=P/2
Пусть MN=2x; KL=7x.
Уравнение
2х+7х=54/2
9х=27
х=3
МN=2x=2*3=6ед.
KL=7x=7*3=21ед.
NK=6x=6*3=18ед.
LM=(MN+KL-NK)=6+21-18=9ед.
ответ: MN=6ед; KL=21ед; NK=18ед; LM=9ед.
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение:
2.В основании ромб, с остым углом 60 градусов, значит высота ромба будет: а*sin60=а корней из 3 разделить на 2. Построим плоскость сечения. Это будет AD1C1B, построим угол наклона этой плоскости к основинию: Проведём два перпендикуляра к ребру АВ -это DP в основании и D1P в плоскости сечения. Найдём высоту призмы: DK*tg60=а корней из 3 на 2 умножить на корень из 3=3а/2. Найдём площадь поверхности: S ромба умножим на 2 , прибавим 3а/2*а*4=6а в квадрате. Сложим полученные величины:6а в квадрате+ площадь ромба, а она равна а квадрат корней из 3 разделить на 2. И так ответ 6а в квадрате +а в квадрате корней из 3.