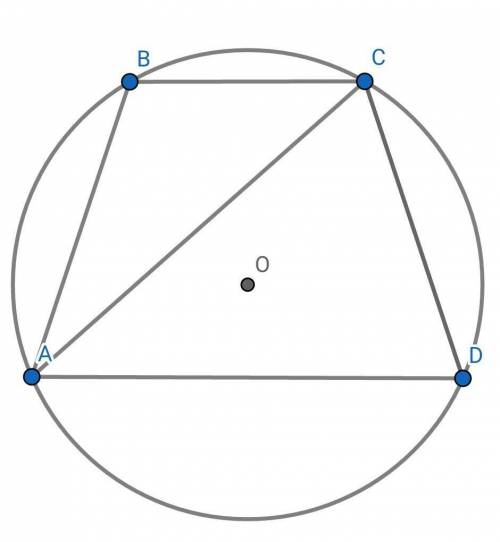
Для начала необходимо помнить, что вписать в окружность можно только лишь равнобокую трапецию. Тогда, АВ = СD = 13 см.
Ну и кроме того, нельзя упускать из виду формулу нахождения радиуса описанной окружности через треугольник. Да-да, треугольник, сейчас всё объясню.
R = (a × b × c) / 4S
Где, а, б и с - стороны треугольника, а S - его площадь.
Т.к трапеция равнобокая, ее диагонали равны. ВD = AC = 20
Рассмотрим ∆АCD.
Найдем его площадь по формуле Герона.
p = 1/2(20+21+13) = 27 см
P.S (p-полупериметр)
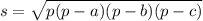
Подставим значения:
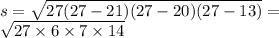
S = 126 см²
Подставим все значения в формулу радиуса:
R = (21 × 20 × 13) / 4×126 = 5460 / 504 = 10 5/6 см
ответ: R = 10 5/6 см (десять целых 5/6 см)
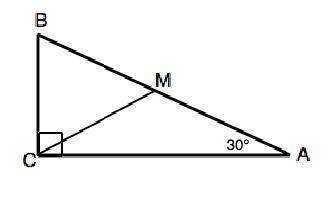
Пусть в прямоугольном треугольнике АВС угол А=30°, угол С=90°. Сумма острых углов прямоугольного треугольника 90°, поэтому угол В=90°-30°=60°
Проведем из прямого угла отрезок СМ так, что угол МСВ=60°.
Тогда в ∆ ВСМ угол СМВ=180°-угол АСВ-угол МВС=180°-2•60°=60°. Углы ∆ВСМ равны, это треугольник равносторонний по определению. ВС=ВМ=СМ.
В ∆ АСМ угол АСМ=90°-60°=30°. Т.к. углы при основании АС равны, то ∆ АМС - равнобедренный по определению, АМ=СМ.
Но СМ=ВМ => АМ=ВМ=ВС. =>
АВ=2ВС, , т.е. катет ВС, противолежащий углу 30°, равен половине гипотенузы, что и требовалось доказать.
х(12-х)=5,5*2
х²-12х+11=0
х1+х2=12 и х1*х2=11
х1=1см-1 часть
х=11см-2 часть