Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
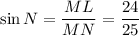
Найти из этого равенства стороны невозможно, потому как в условии нет ни одного линейного размера. Например, стороны могут быть равны:
ML = 24, MN = 25
Или увеличенные в любое количество раз:
ML = 24 · 2 = 48; MN = 25 · 2 = 50
ML = 24 · 3 = 72; MN = 25 · 3 = 75
ML = 24 · 0,2 = 4,8; MN = 25 · 0,2 = 5
ответ: зная только синус острого угла прямоугольного треугольника, невозможно найти ни одну сторону этого треугольника, можно только указать их отношение.
Номер 1
<А=<43=43 градуса,как вертикальные углы
Треугольник АВС равнобедренный,т к по условию задачи внешние вертикальные углы равны между собой,а значит и внутренние тоже равны между собой
<ВАС=<ВСА=43 градуса
<В=180-43•2=180-86=94 градуса
Номер 3
<1+<2=180-28=152 градуса
8+11=19 частей
Одна часть равна
152:19=8 градусов
<2=8•11=88 градусов
Номер 5
<АМВ+<ВМС=180 градусов,как смежные
<ВМС=180-70=110 градусов
По условию задачи треугольник ВМС равнобедренный,тогда
<МВС=<С=(180-110):2=70:2=35 градусов
<АВМ=<МВС=35 градусов,по условию задачи
<В=35•2=70 градусов
<А=180-(70+35)=180-105=75 градусов
Номер 7
<МНР+<РНК=180 градусов,как смежные
<МНР=180-80=100 градусов
<МРН=<НРК=70:2=35 градусов
<М=180-(100+35)=180-135=45 градусов
Объяснение: