ответ: 30°
Объяснение: Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
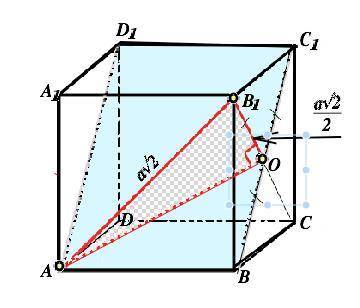
Искомый угол - угол между диагональю АВ1 боковой грани АВВ1А1 и плоскостью АВС1D1.
Проекция АВ1 - отрезок АО, где О - точка пересечения диагоналей квадрата - грани ВСС1В1, которые пересекаются под прямым углом. .
Если ребро куба принять равным а, то по формуле диагонали квадрата АВ1=а√2, , а В1О=0,5а√2. В прямоугольном ∆ АОВ1 катет В1О, противолежащий искомому углу В1АО, равен половине гипотенузы АВ1. => sin(ВАО)=1/2=> угол между прямой AB1 и плоскостью ABC1 равен 30°
прямая y=kx+m
из первого уравнения 0*k+m=1, m=1
для второго k*(-4)+1=-5
-4k=-6
k=1,5
Следовательно, y=1,5x+1