Объяснение:
а) Рассмотрим треуг. АВЕ и СВД.
АВ = ВС как боковые стороны равнобедренного треуг. АВС. ВЕ = ВД как половинки боковых сторон равнобедренного тр-ка АВС (т.к. АЕ и СД медианы). Угол В у этих тр-ков общий. Следовательно тр-ки АВЕ = СВД по первому признаку.
б) Рассм. тр-ки ДОЕ и АОС.
В равнобедренном тр-ке медианы, проведенные из вершин при основании к боковым сторонам равны и медианы пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1 считая от вершины. Значит АЕ = СД, ОД = ОЕ = 1/3 АЕ, АО = ОС = 2/2 АЕ. Треугольник, у которого две стороны равны, называется равнобедренным. Следовательно тр-ки ДОЕ и АОС равнобедренные.
в) Повторюсь, медианы треугольника пересекаются в одной точке (эта точка называется центроид). Значит точка О лежит на медиане, проведенной из вершины В к основанию. Но медиана, проведенная из вершины равнобедренного треугольника к основанию является также и бисектриссой. Значит точка О лежит на бисектриссе, а точки Д и Е принадлежат боковым сторонам равнобедренного тр-ка АВС, следовательно ВО бисектрисса угла ДОЕ.
2. У равных тр-ков равны соответствующие стороны и углы.
Пусть DE = DF = 4 см - боковые стороны, FE = 5 см - основание, тогда периметр
DEF = 4 + 4 + 5 = 13 см. И как было сказано вначале, что у равных тр-ков равны соответствующие стороны, то АС = АВ = 4 см, ВС = 5 см. Р = 13 см.
Но может быть и другой вариант решения, поскольку в задаче не указано какая из сторон является основанием, а какая боковая, поэтому.
EF = DF = 5 см - боковые стороны, DE = 4 см - основание, Р = 5 + 5 + 4 = 14 см.
Следовательно периметр тр-ка АВС = 14 см.
4.
Дано:
ABC - прямоугольный треугольник
AB = 5см
BC = 12см
AC - гипотенуза
BD - высота, опущенная на гипотенузу AC
Для начала вычислим длину гипотенузы AC, воспользовавшись теоремой Пифагора:
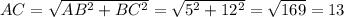
Опустив высоту AD на гипотенузу AC у нас получилось два прямоугольный треугольника - ABD с гипотенузой AB и BCD с гипотенузой BC. Пусть AD = x, тогда DC = 13 - x, так как AC = 13 см.
Поскольку высота AD является общим катетом для треугольников ABD и BCD запишем:
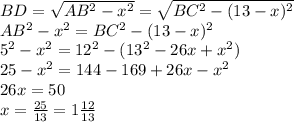
Итак, AD = x = 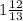 см., а DC = 13 - x =
см., а DC = 13 - x = 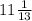 см.
см.
Найдём высоту BD:
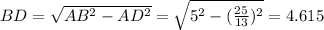 см.
см.
Высота BD делит гипотенузу AC на отрезки 1 12/13 см. и 11 1/13 см.
Высота BD равна 4,615 см.
(странные какие-то цифры, но я перепроверил решение несколько раз - всё сходится вроде бы...)
5.
Косинус угла равен отношению прилежащего катета к гипотенузе.
AB является гипотенузой. Следовательно:
cos(30) = 2 / AB
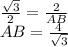
по теореме Пифагора
АН^2=AC^2-CH^2
AH=6
треугольник АСН и АВС подобны по двум углам: одному прямому и одному общему при вершине А (НАС=САВ)
=>AH/AC=AC/AB
AB=937,5
sinABC=75/937,5=0,08