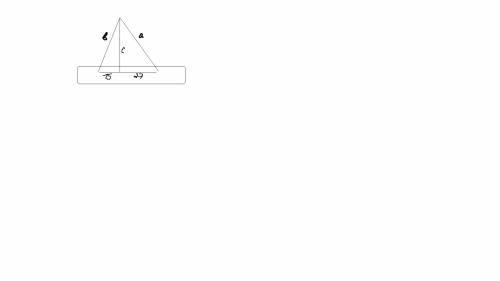
Рассмотрим плоскость ABD (по А1 существует плоскость ABD). ME- средняя линия треугольника ABD по определению. По А1, BK - середина треугольника BDC (по определению). PK||BD, PK=DB÷2 => PK||DE (по теореме о параллельных прямых). PK=ME=DB%2. По А1: существует такая плоскость MPKE-параллелограм (по первому признаку параллелограмма). MK, De-диагональ, MK=PE (по условию). По А1: MP-средняя линия треугольника ABC. Треугольник EMP-прямоугольный => по теореме Пифагора найдём ME^2=EP^2-MP^2=10^2 - 6^2 =8^2 => ME=8, тогда BD=2*8=16. ОТВЕТ: BD=16
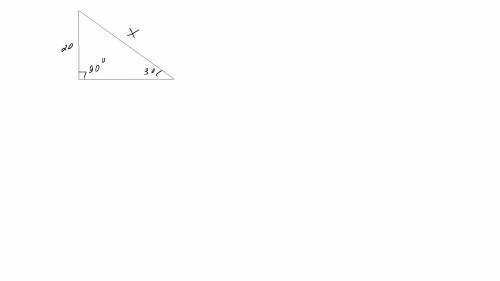
4) по теореме синусов получаем извняюсь перепутал
x/sin90=20/sin30
x=40
ответ 40 см
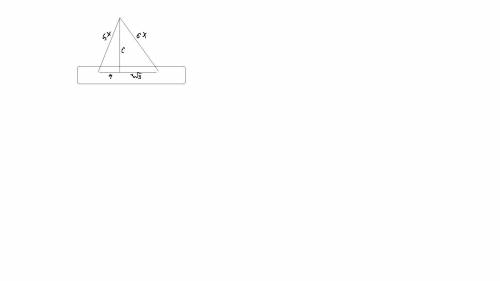
5(1) пусть Сторона равняються а и в
тогда
{a-b=6
{b^2-a^2=15^2-27^2
{a=6+b
{b^2-(36+12b+b^2)=-504
{b^2-36-12b-b^2=-504
{ -12b=-504+36
{b=39
{a=45
Значит сама длина равняеться C=V39^2-225=V1296=36
ответ длина равняеться 36см
5(2)
пусть первая сторона 5х тогда вторая 6х
По теореме Пифагор
36x^2-27=25x^2-16
11x^2=11
x=1
Значит длина равняеться 5^2-4^4=3^2
ответ длина равняеться 3см
6) щас решу
2x^2=256
x=8V2
Половина
y=V128-64=8
y2=V17^2-8^2=15
искомая равна =V(8^2+15^2-2*8*15cos60)=13